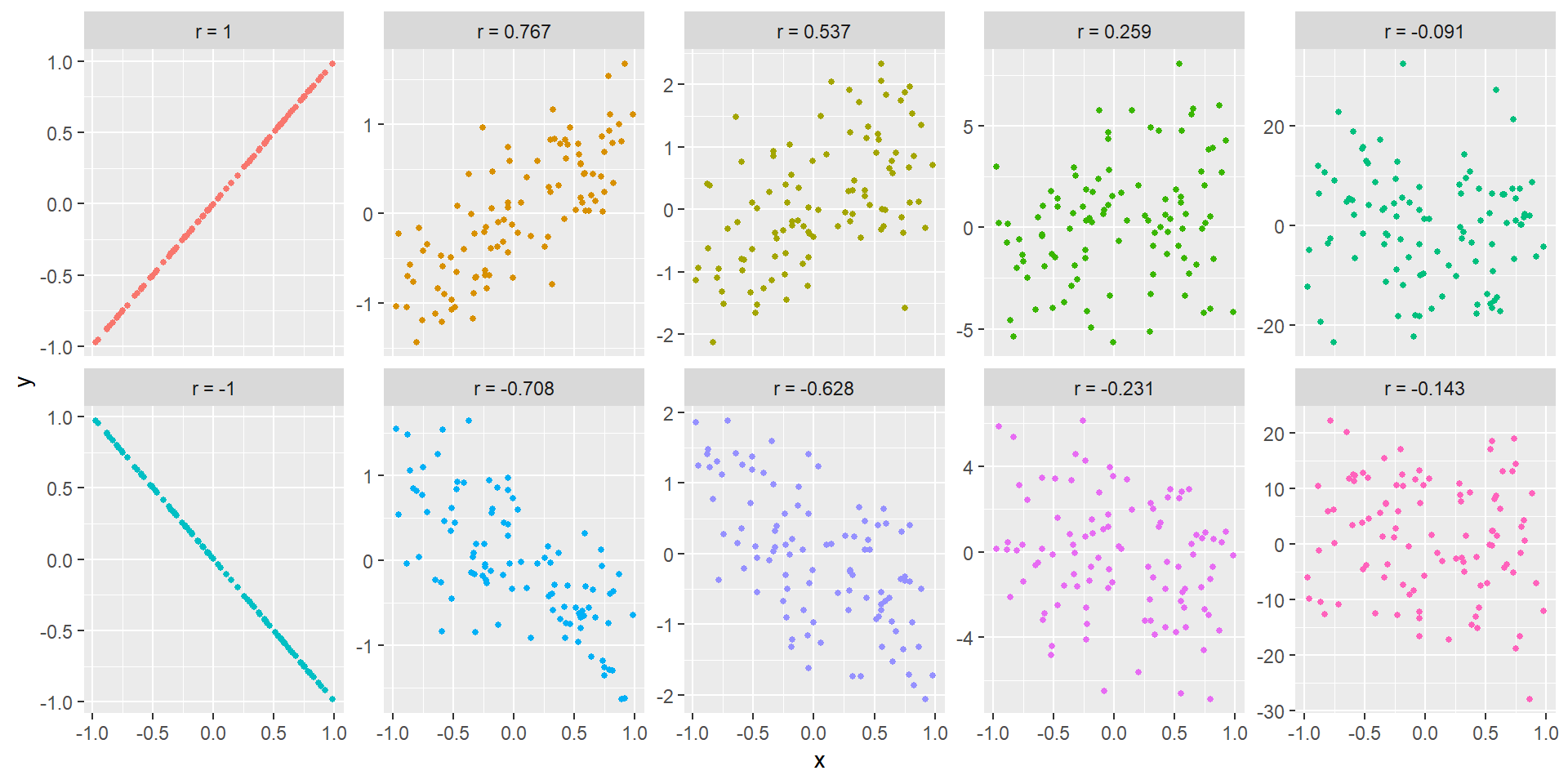
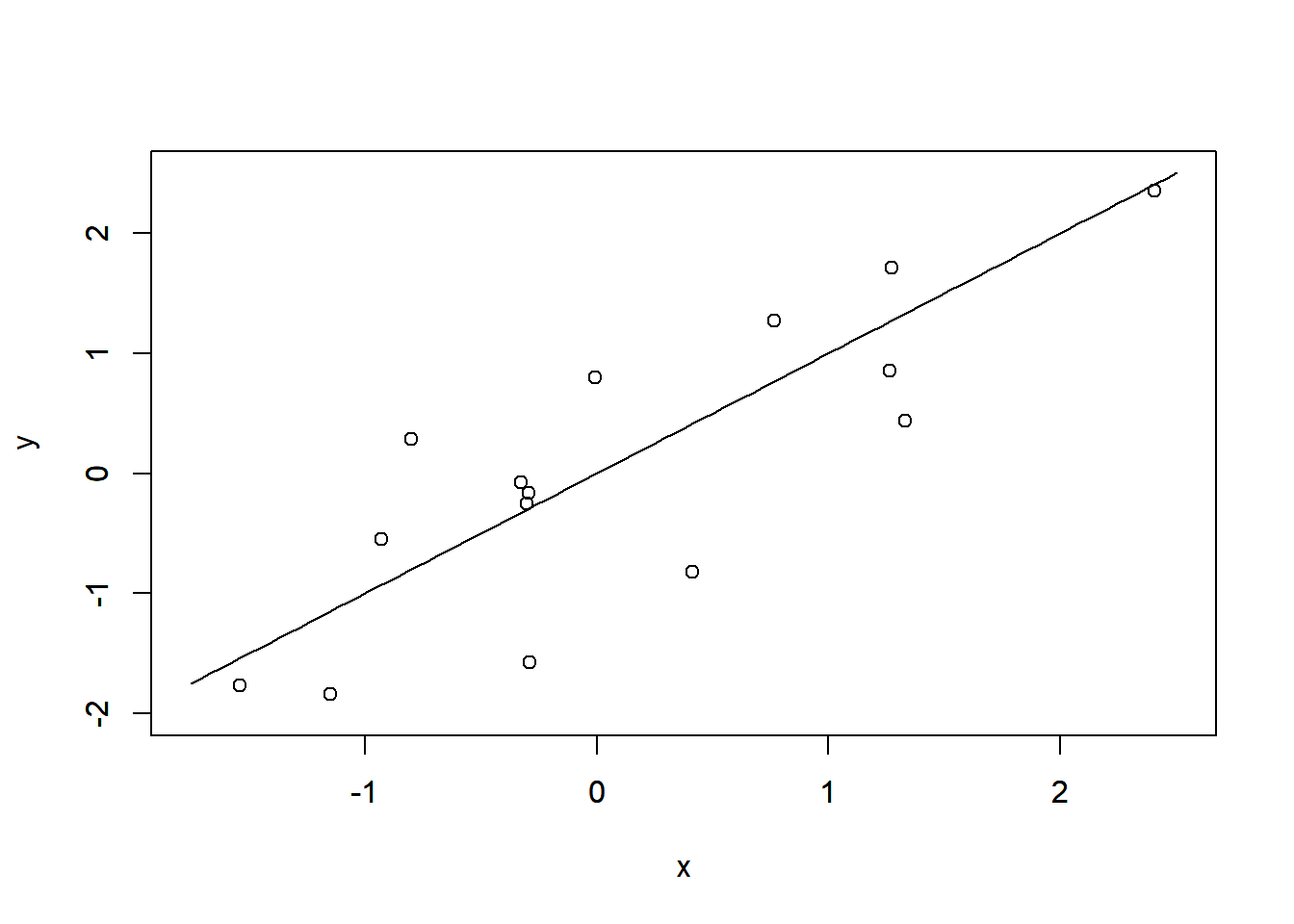
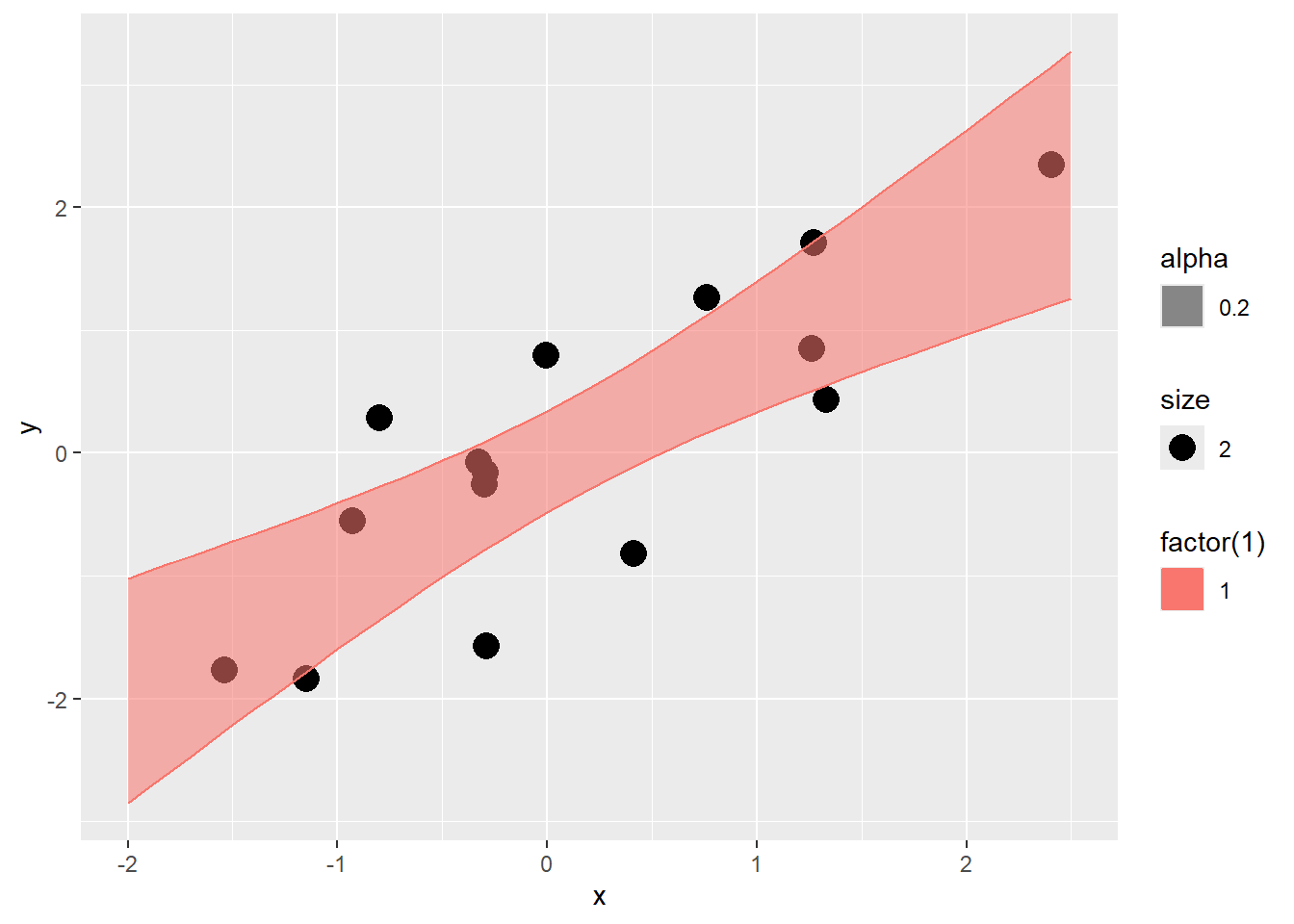
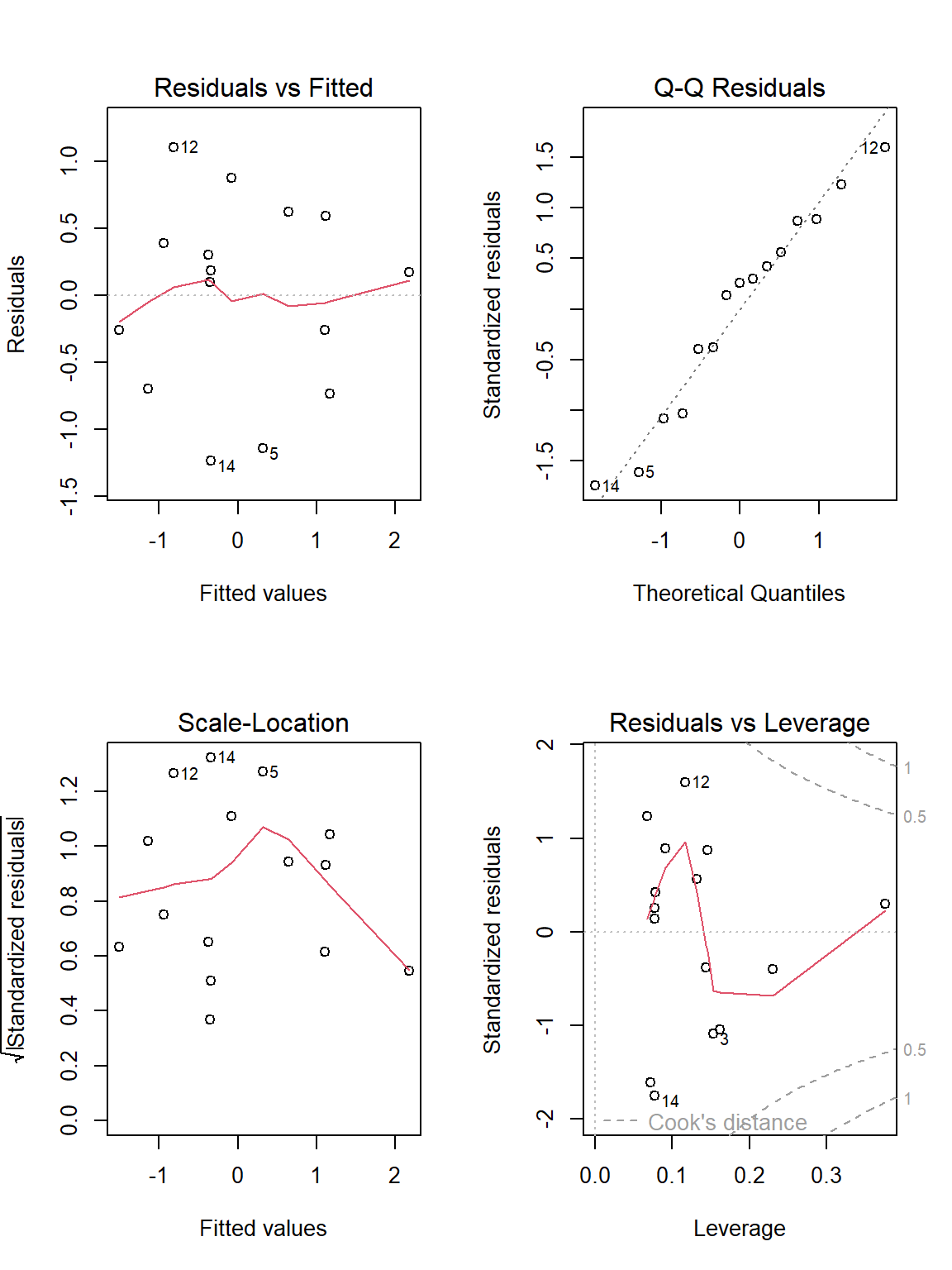
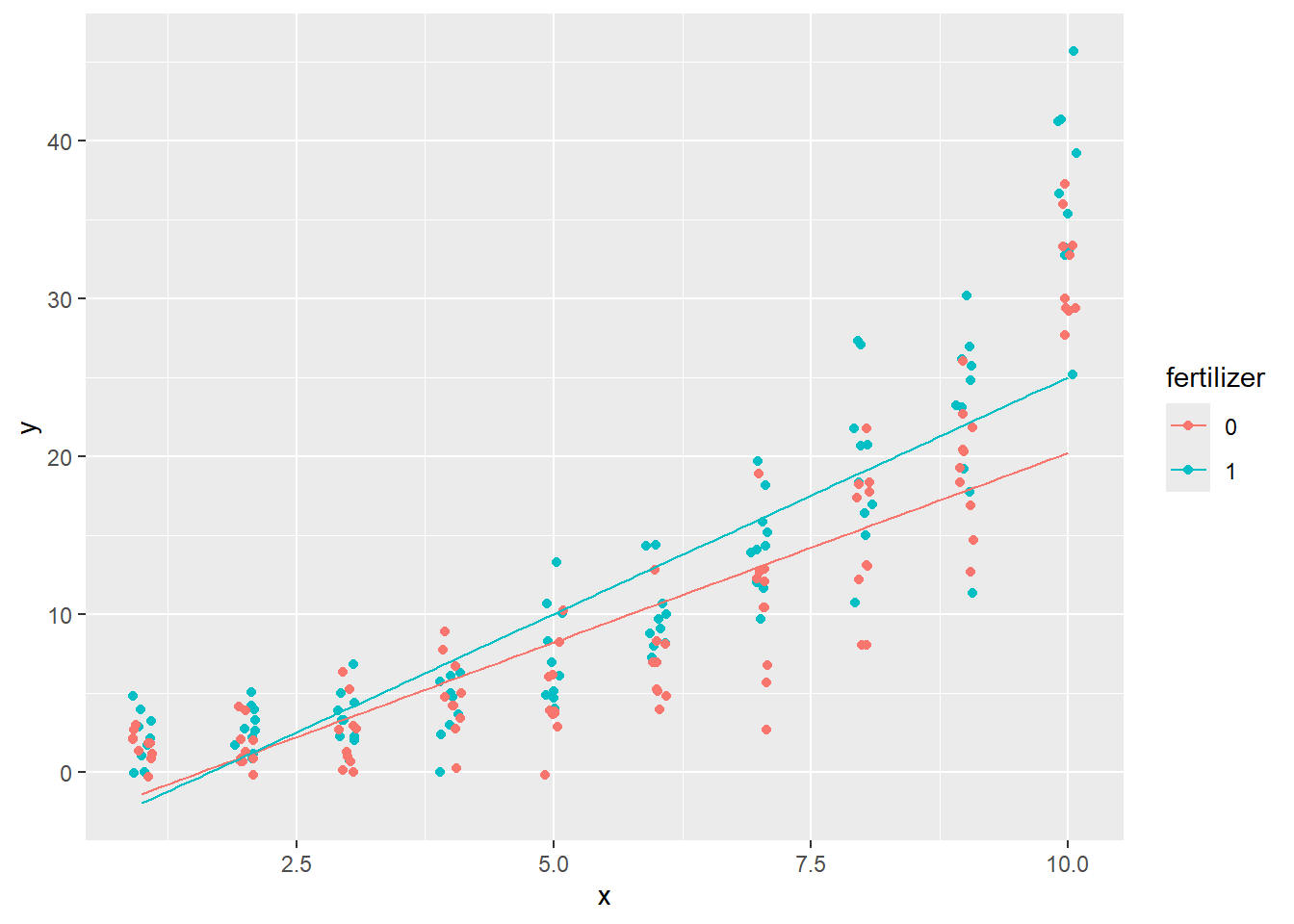
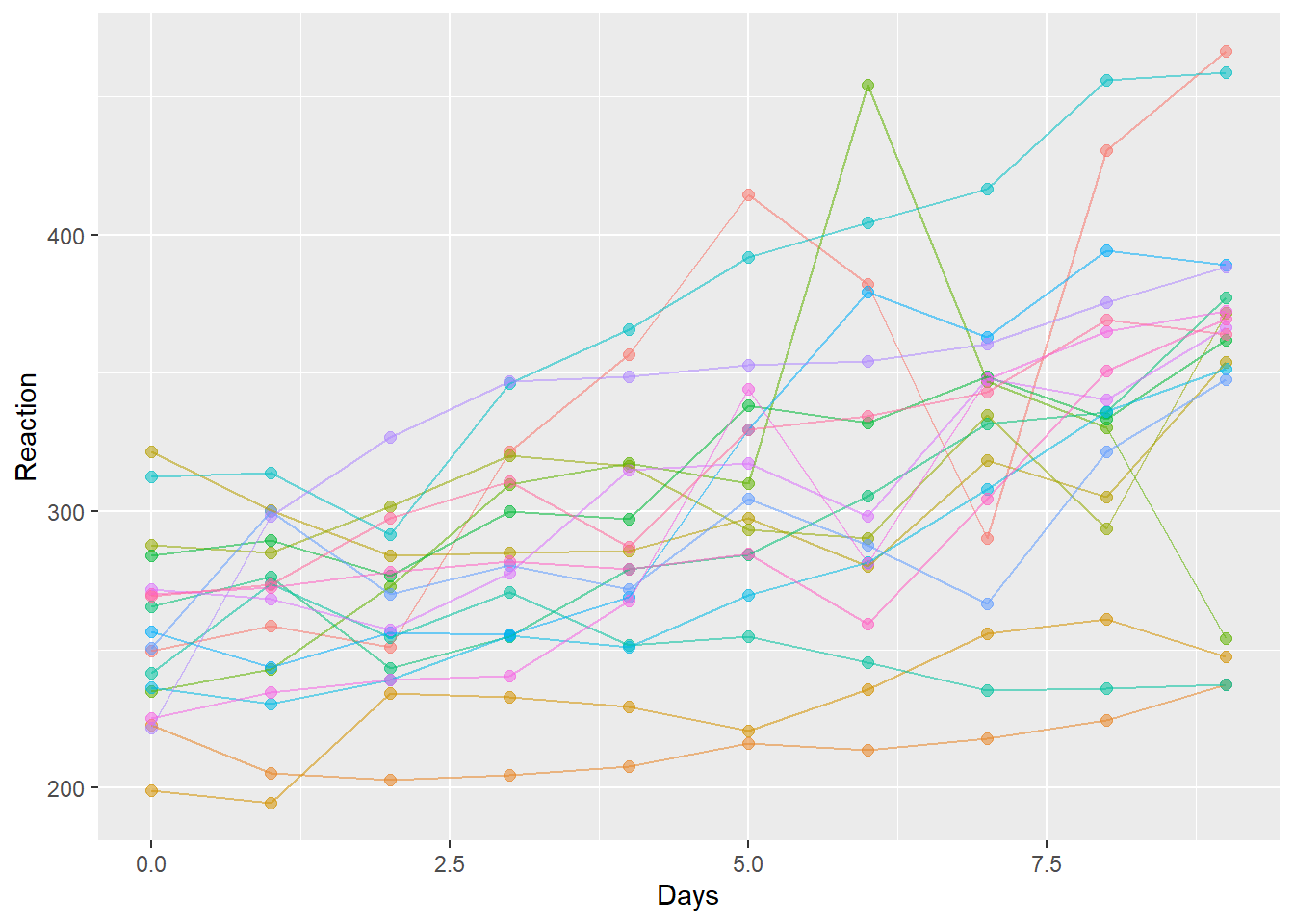
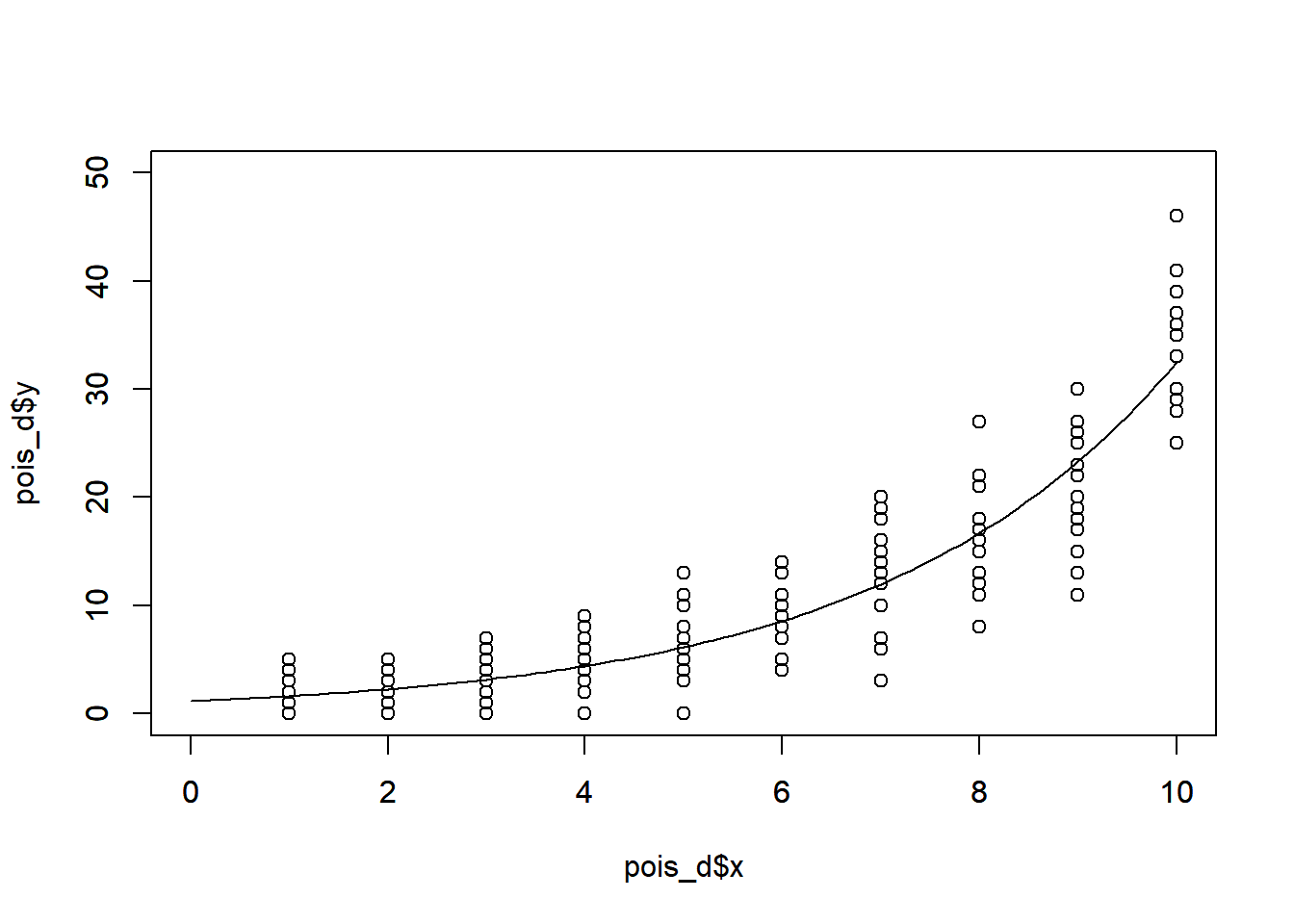
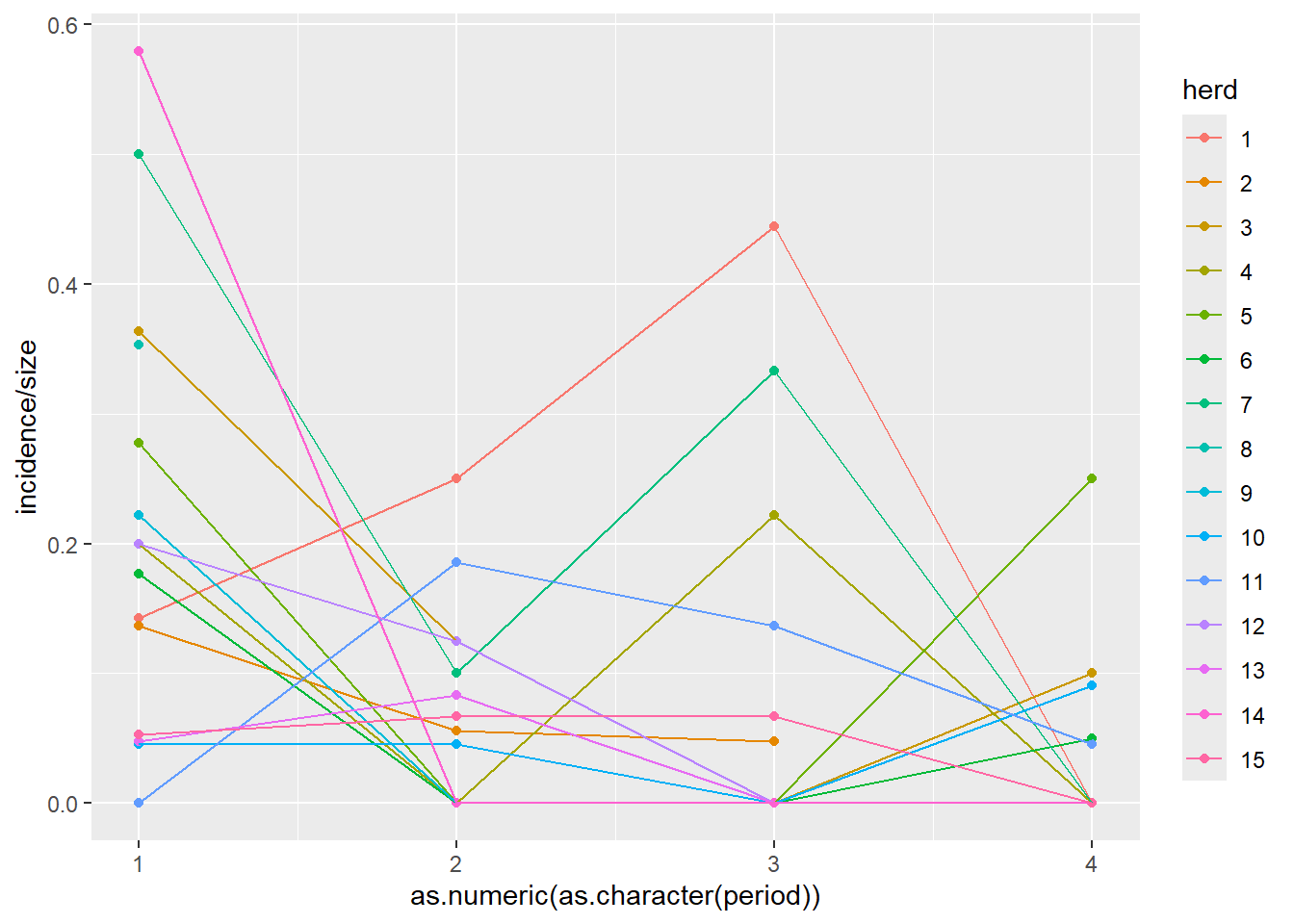
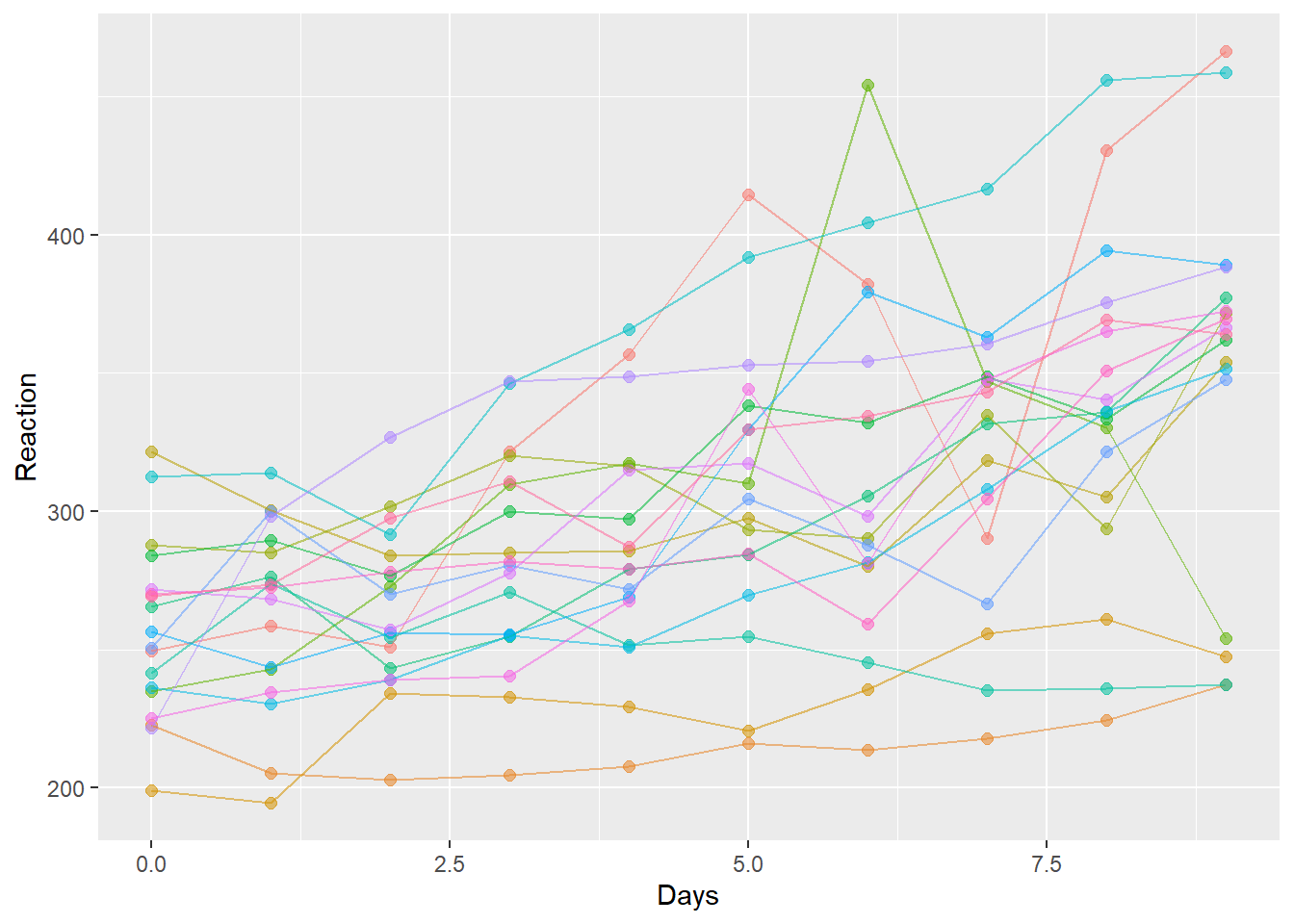
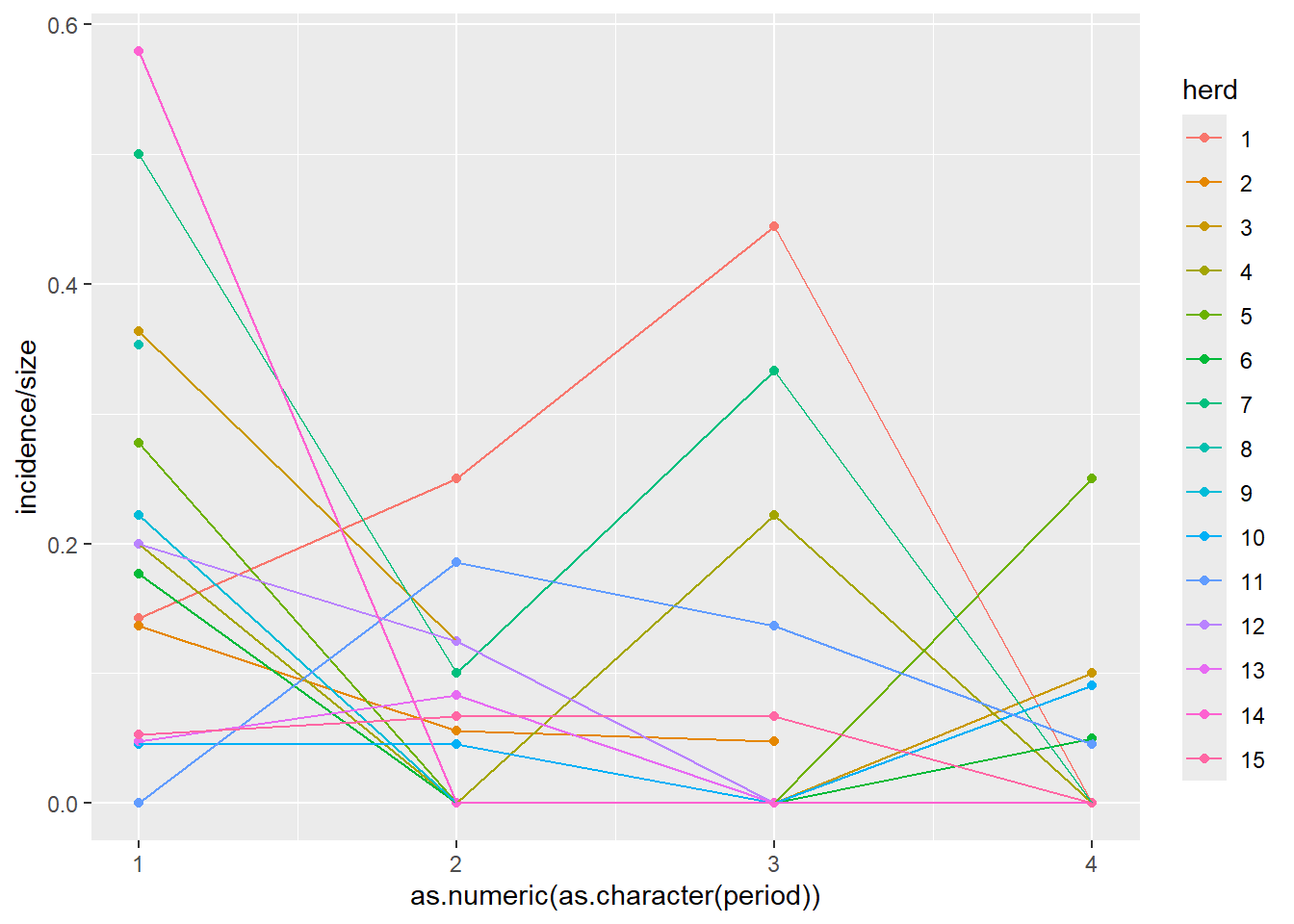
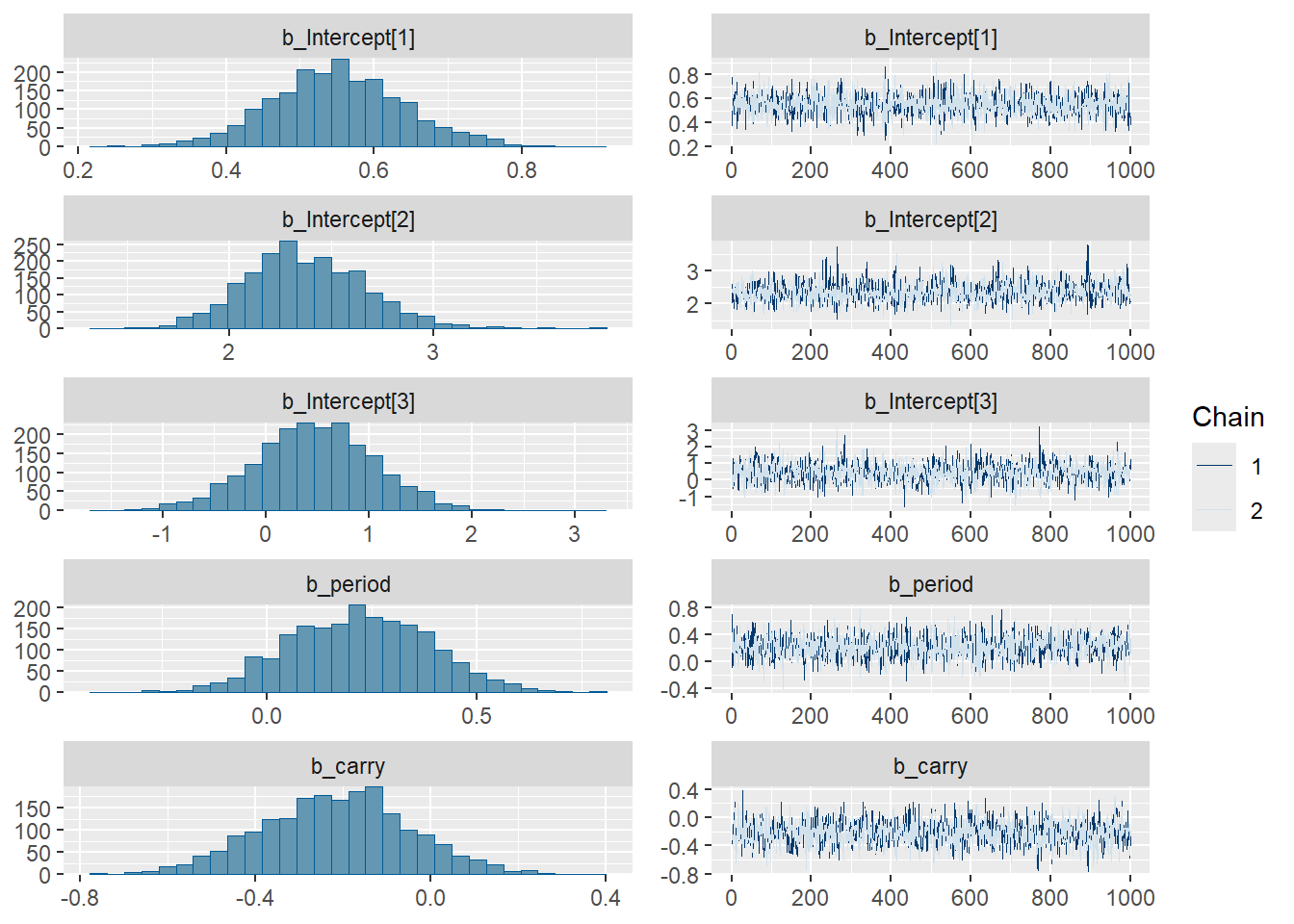
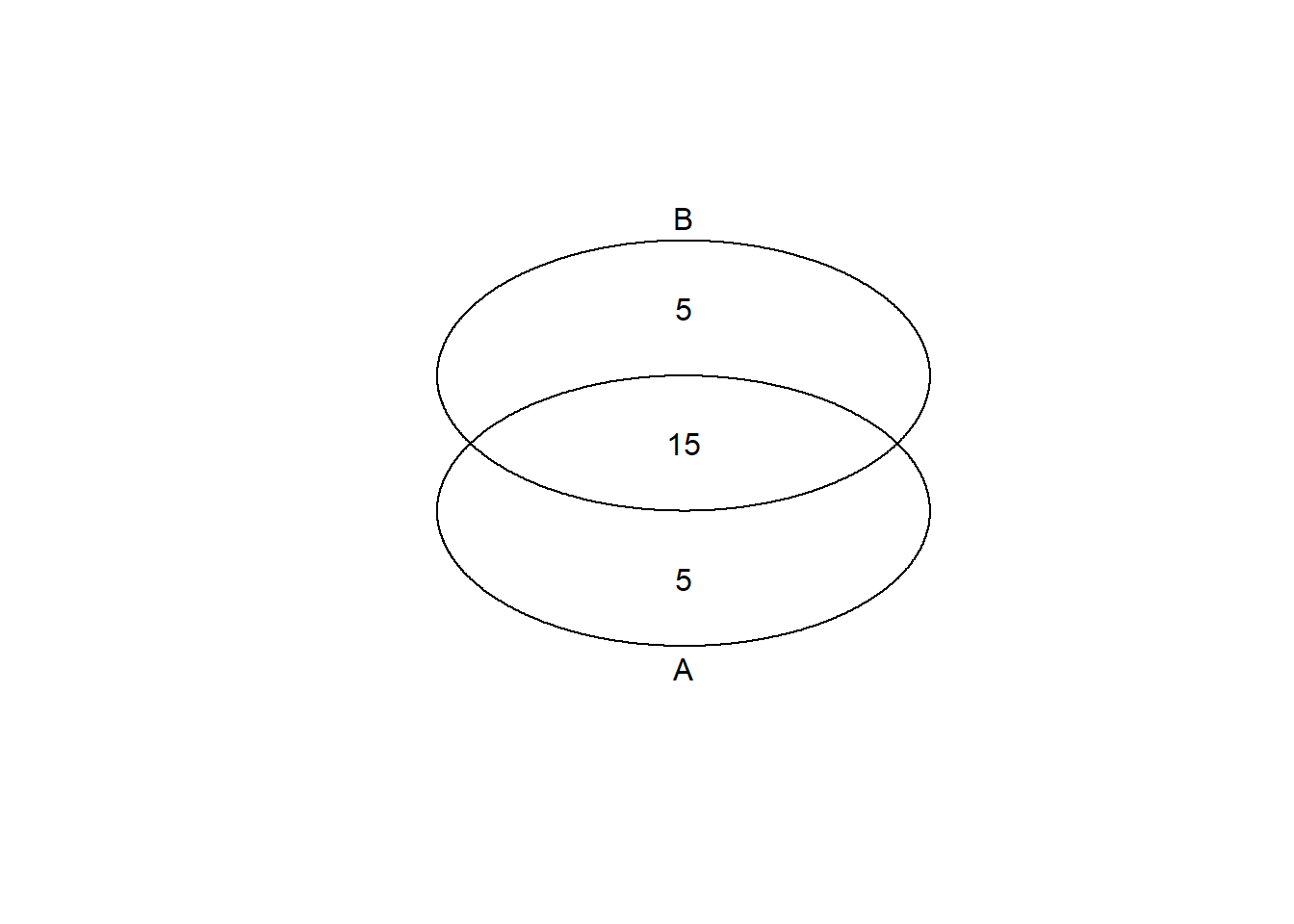
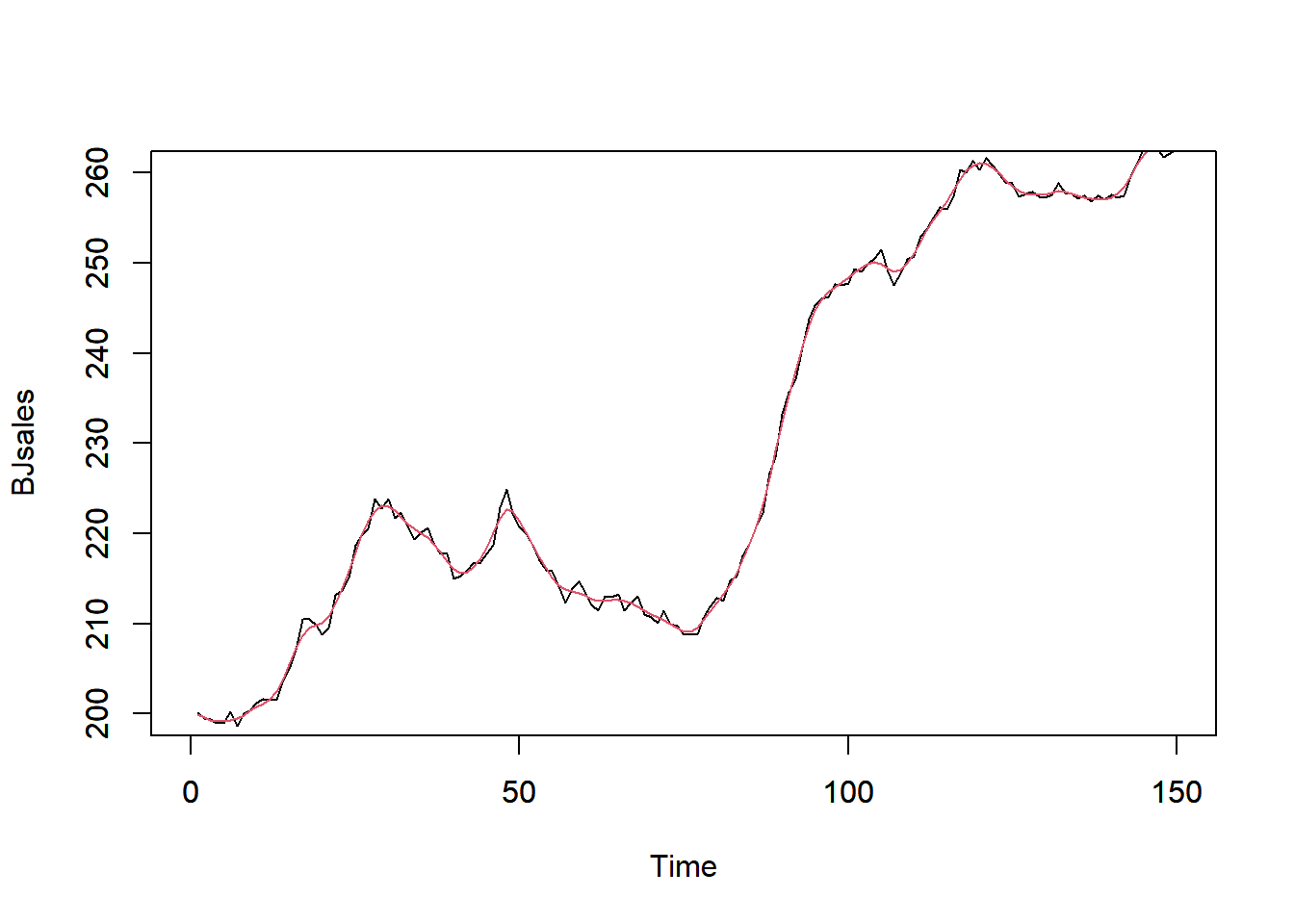
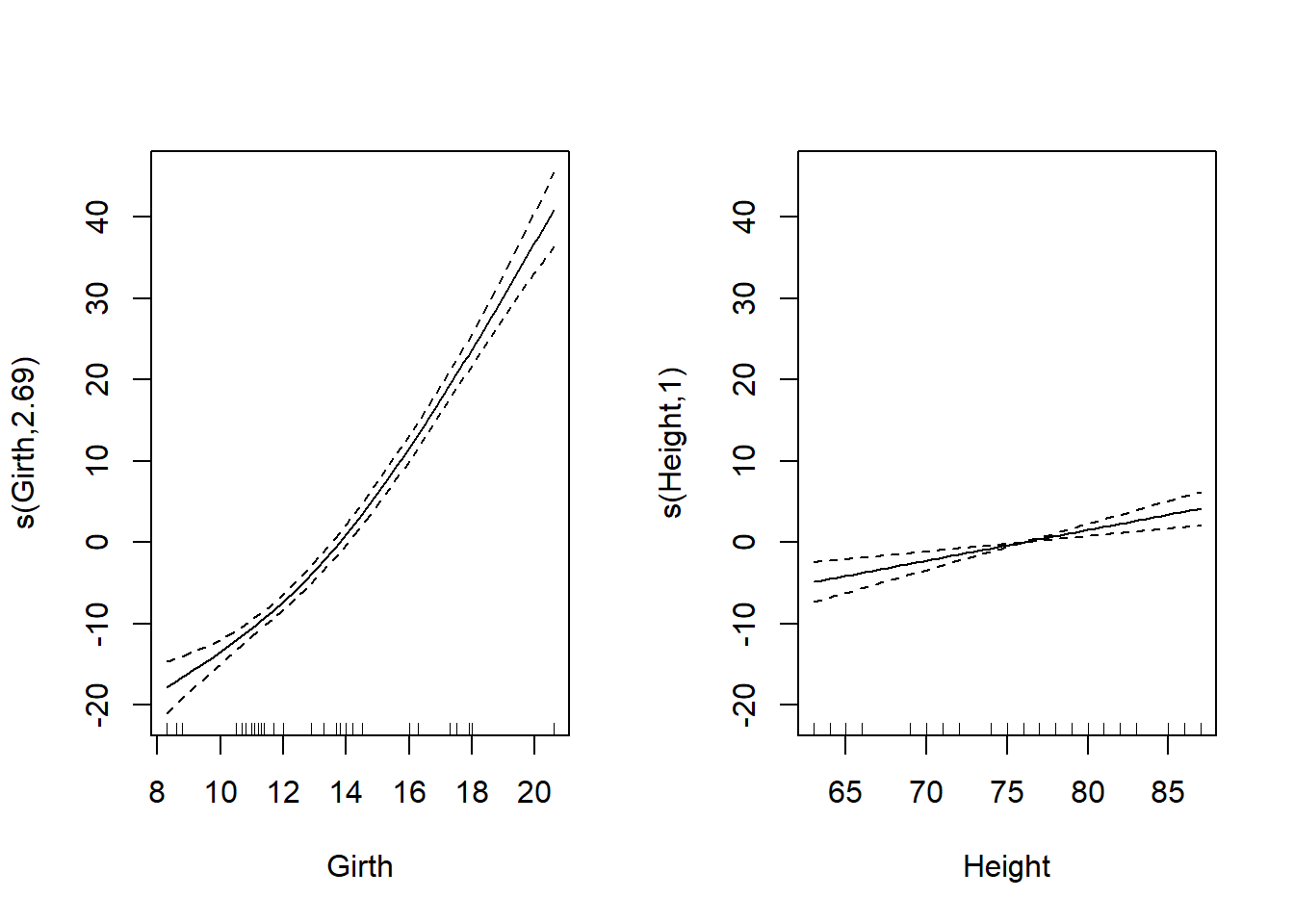
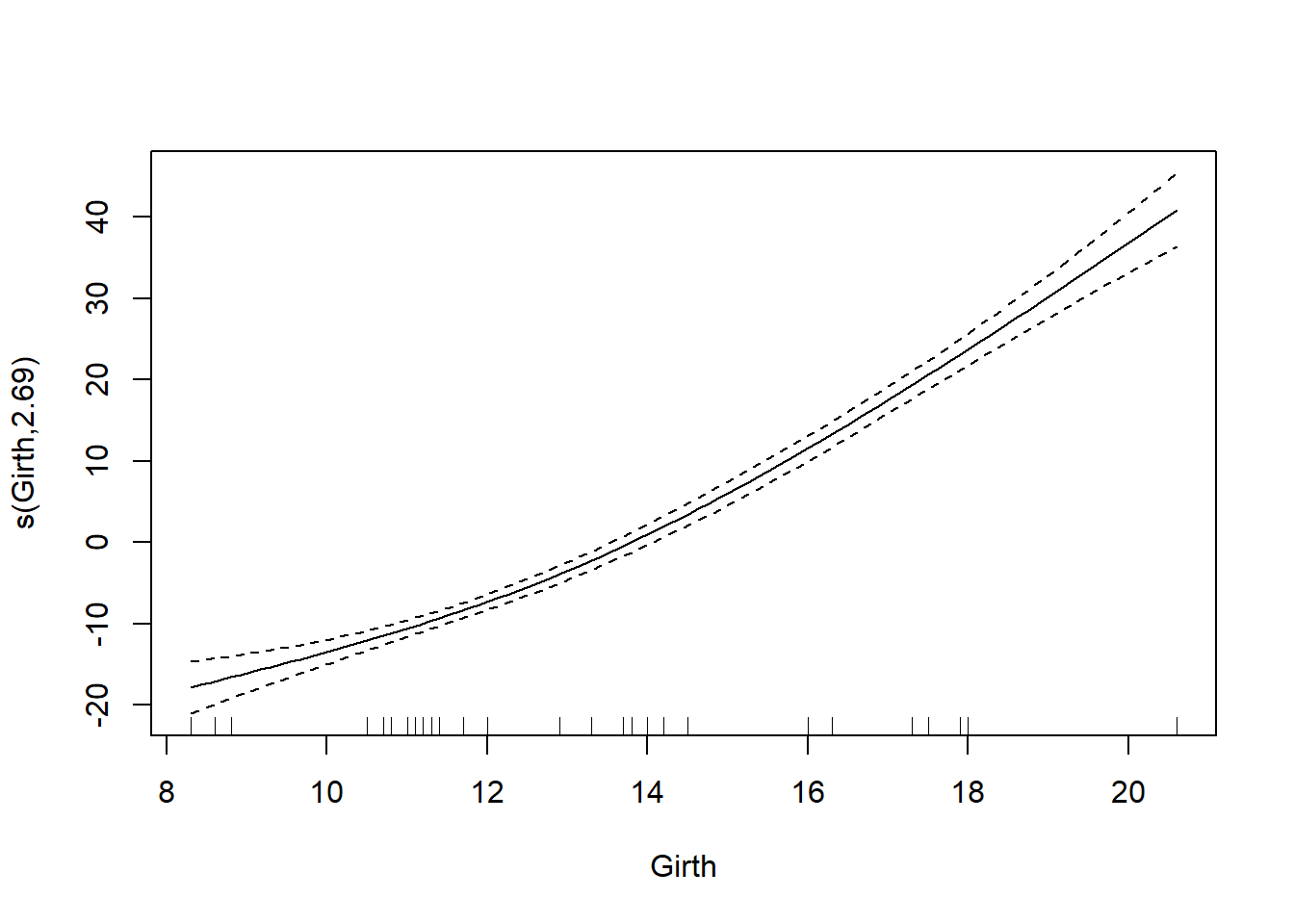
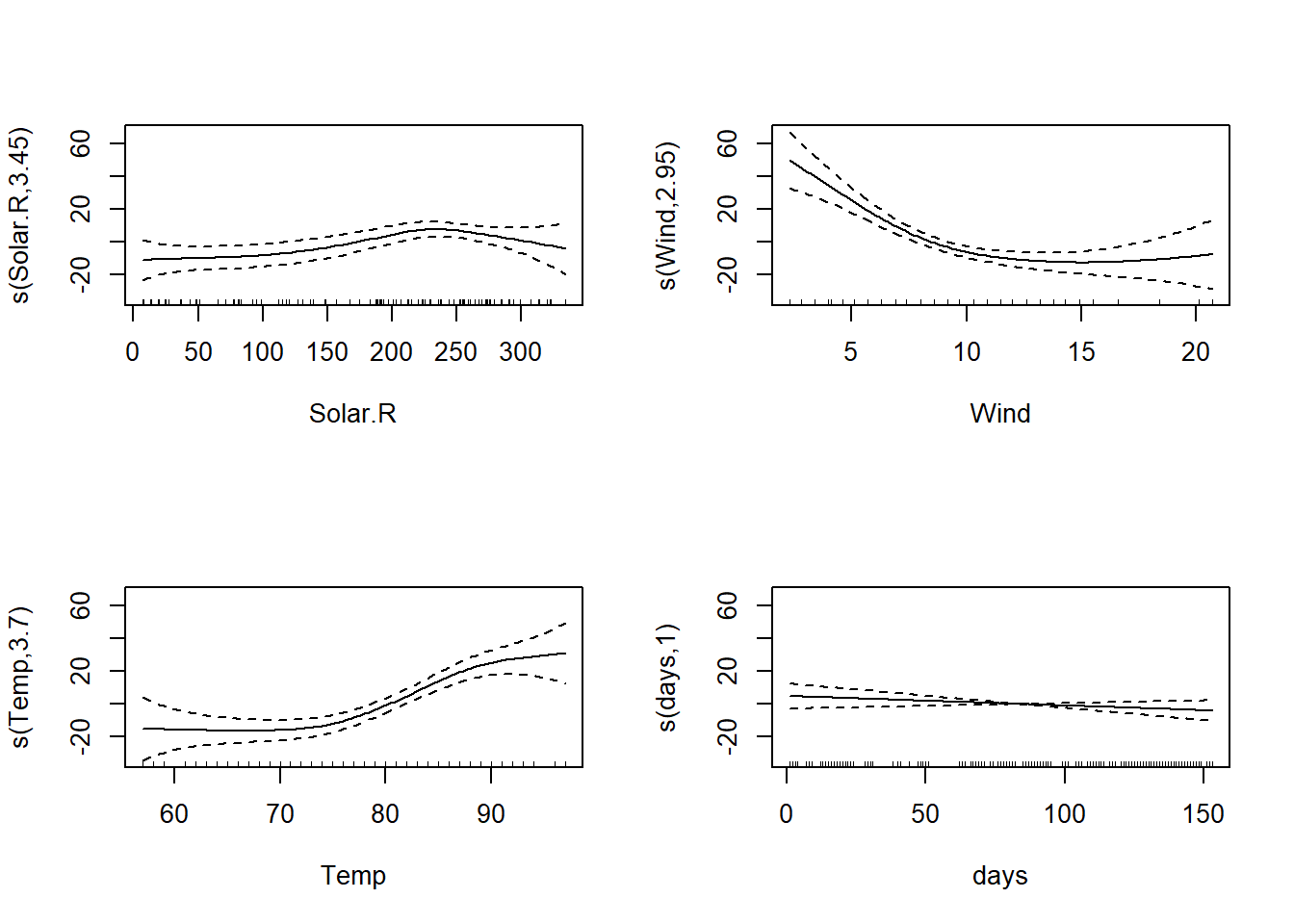
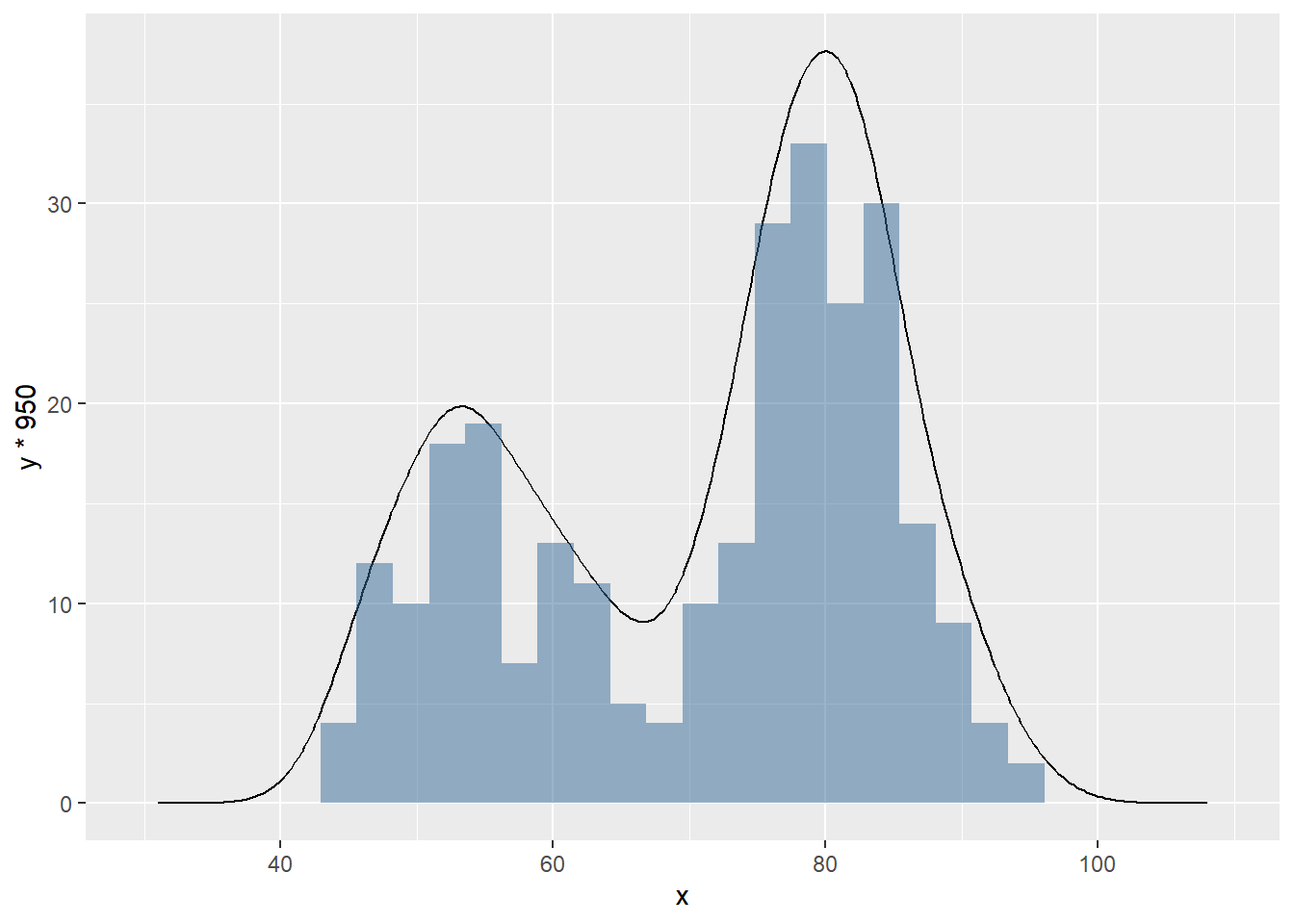
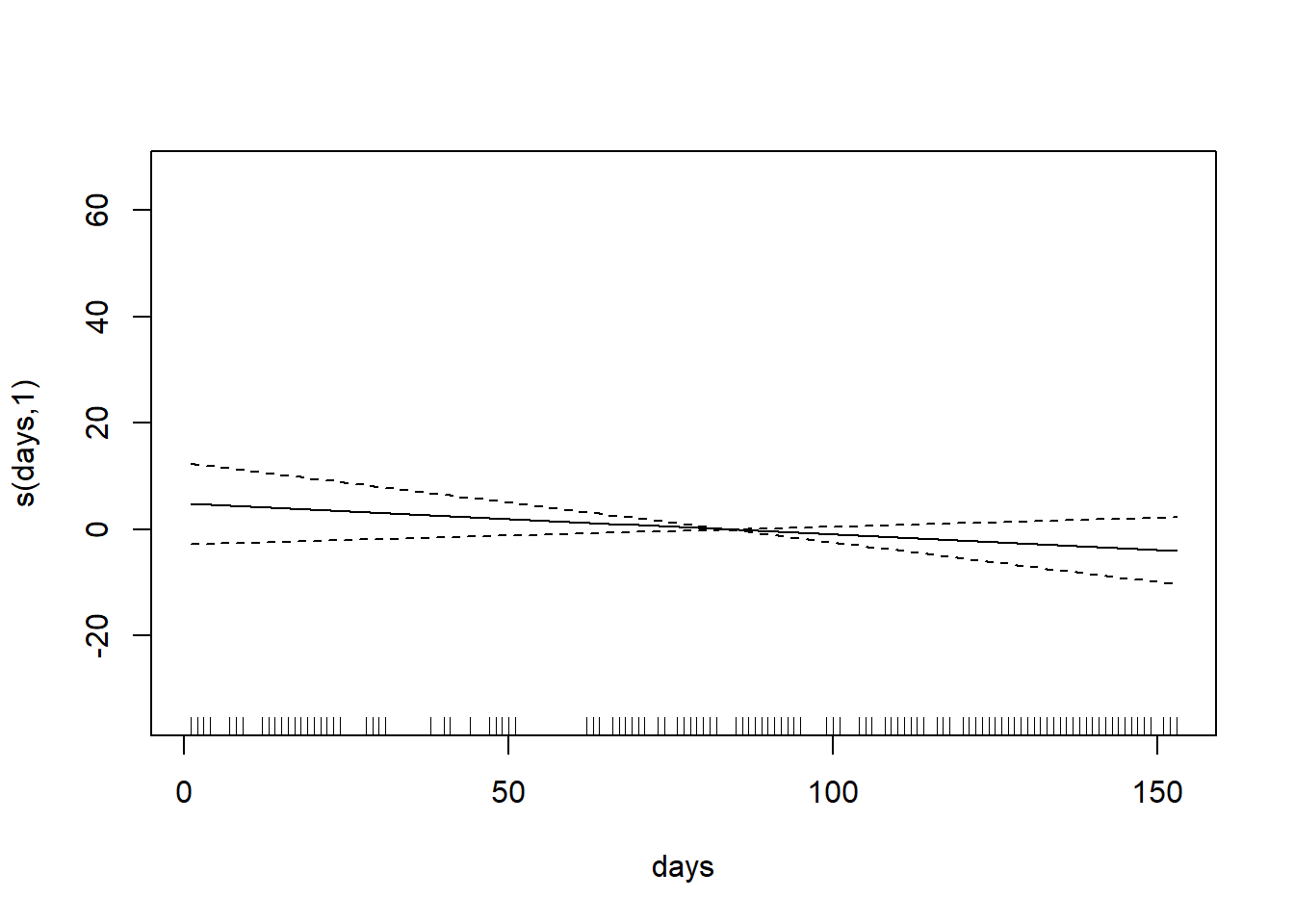
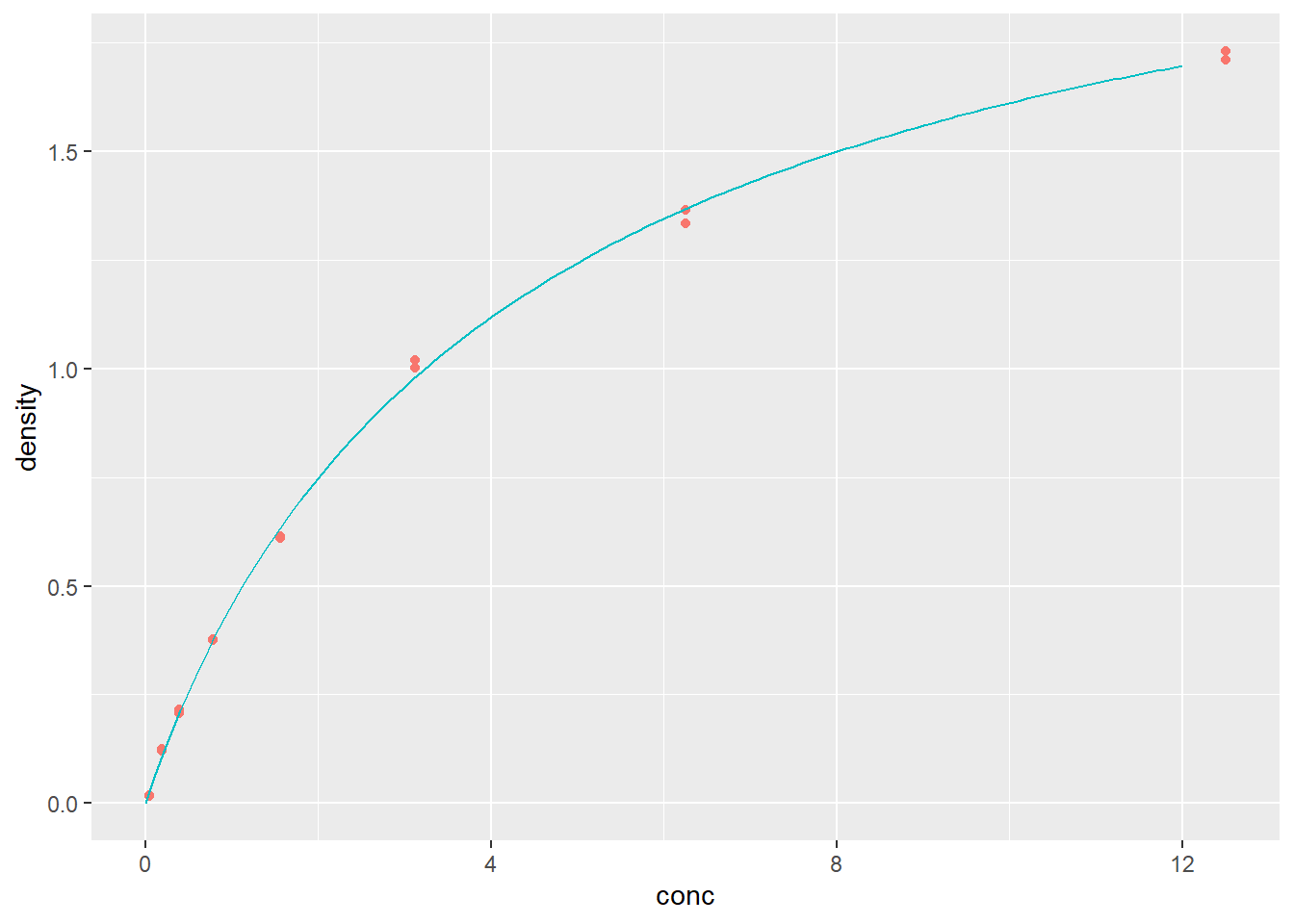
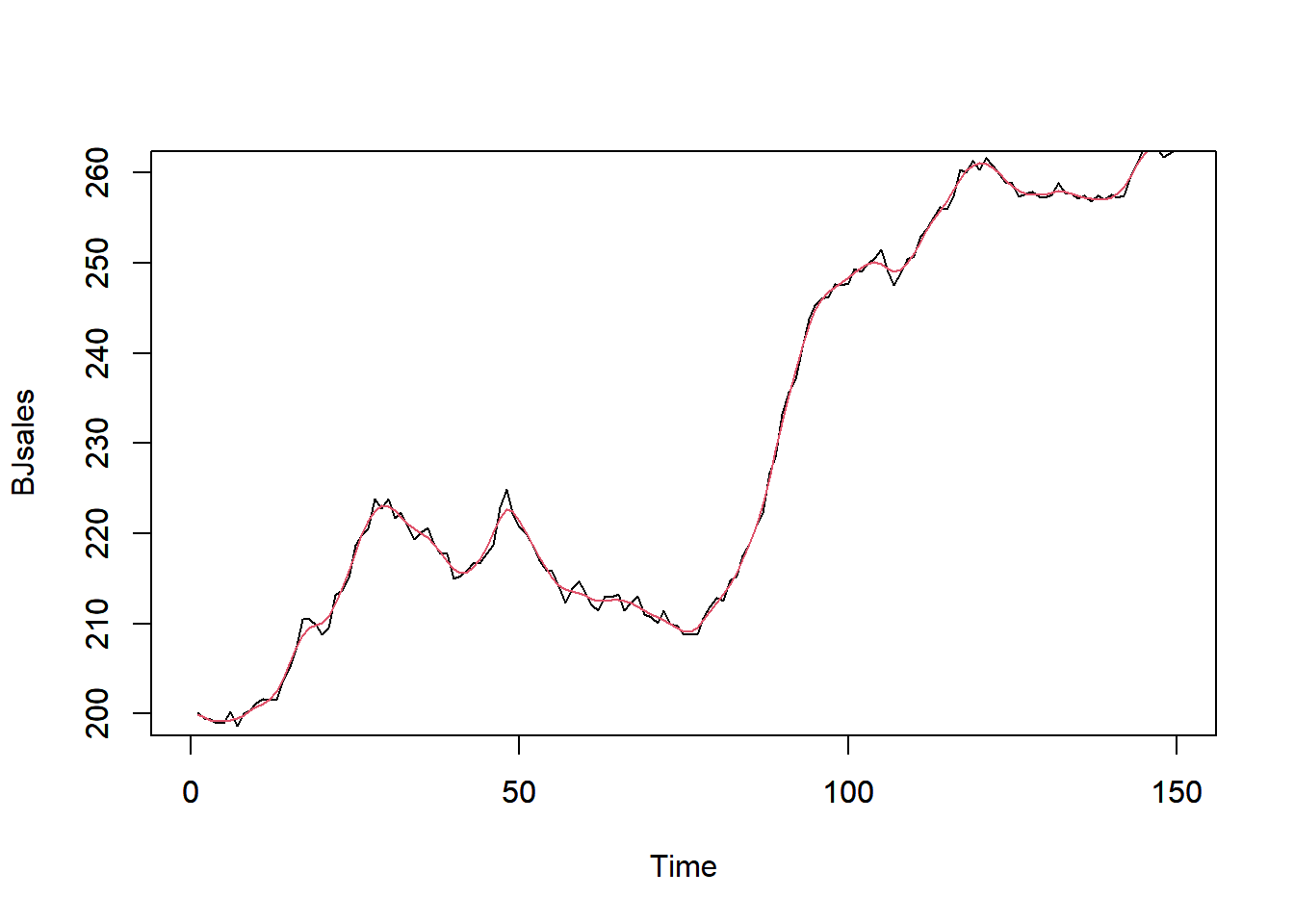
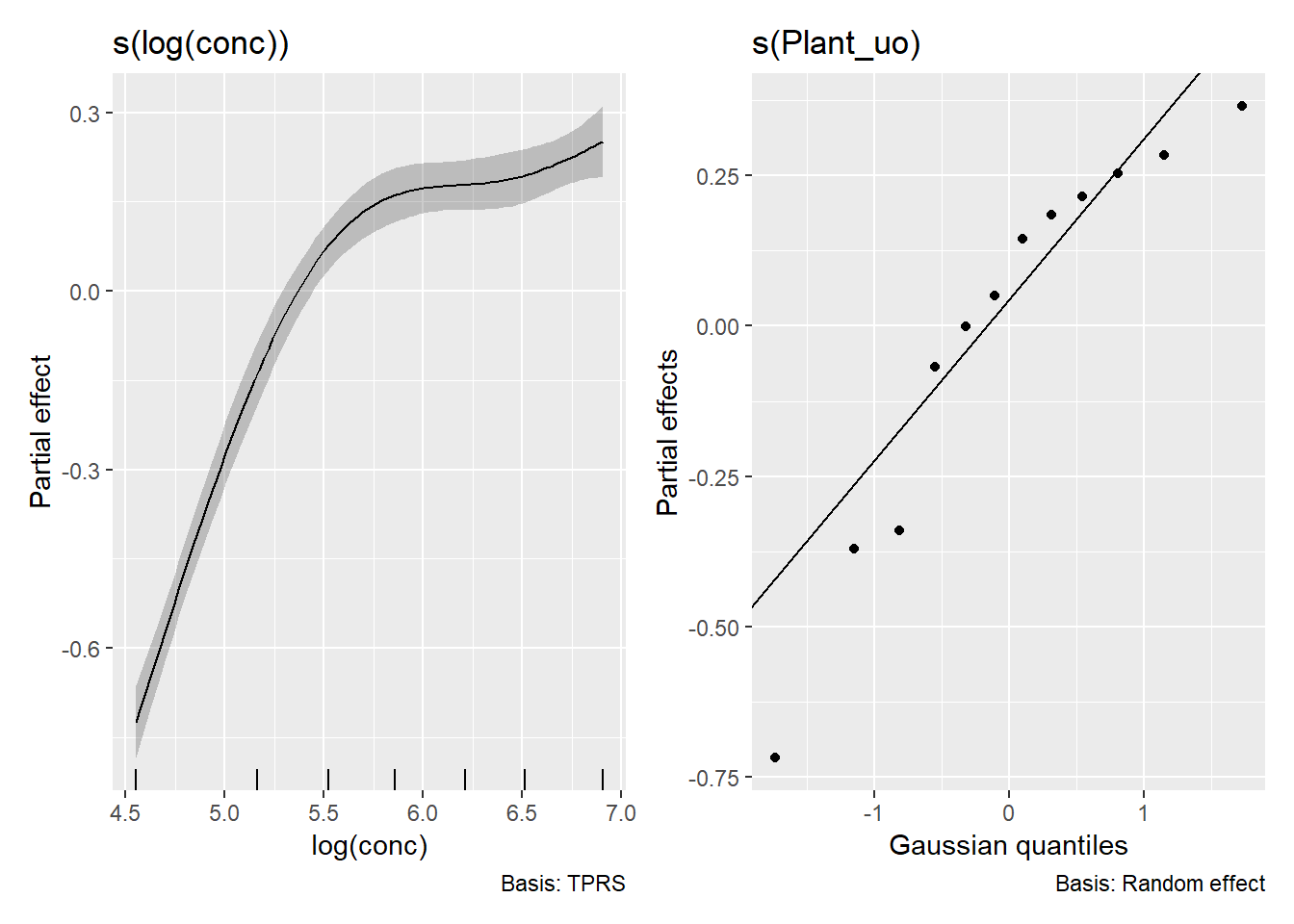
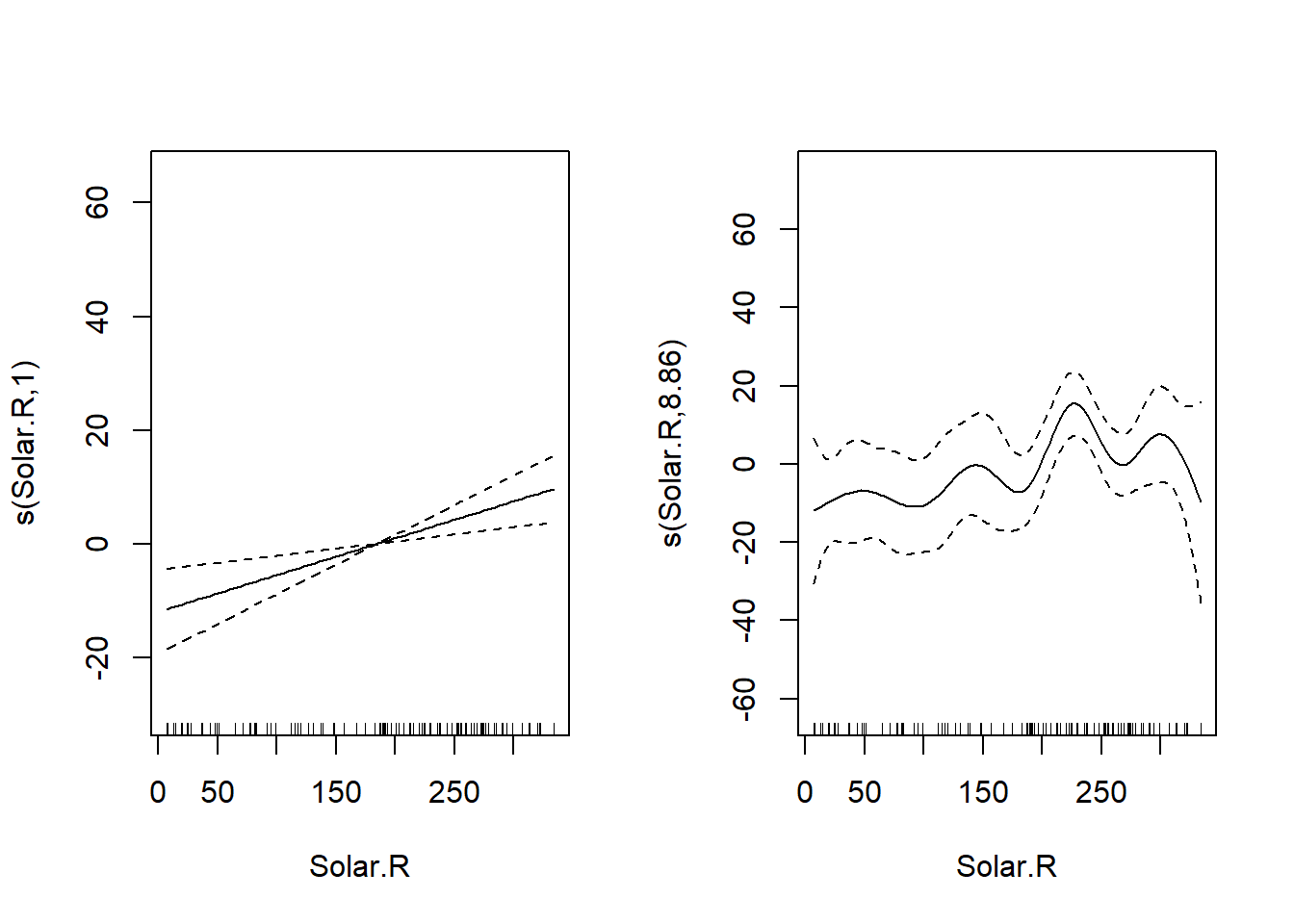
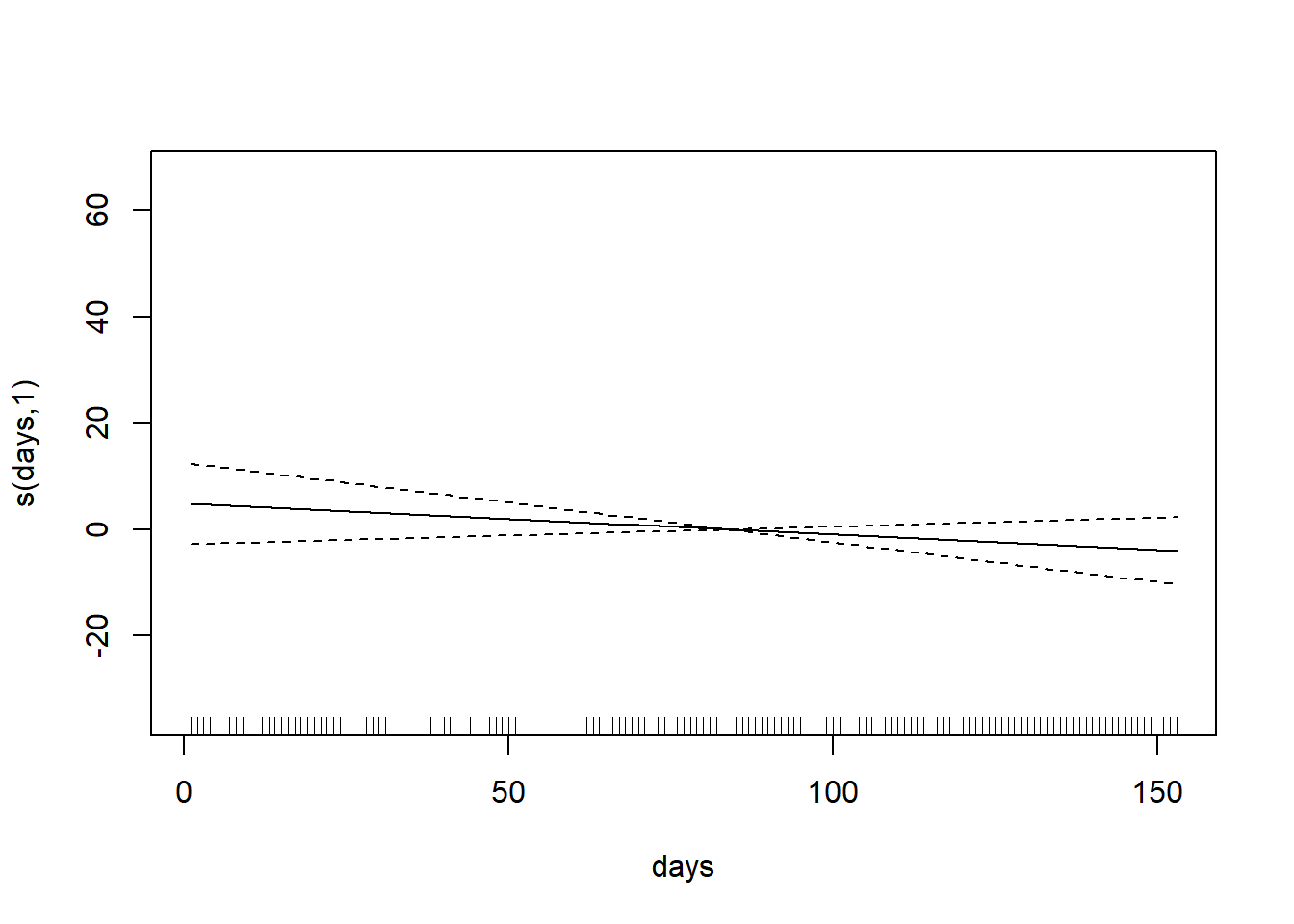
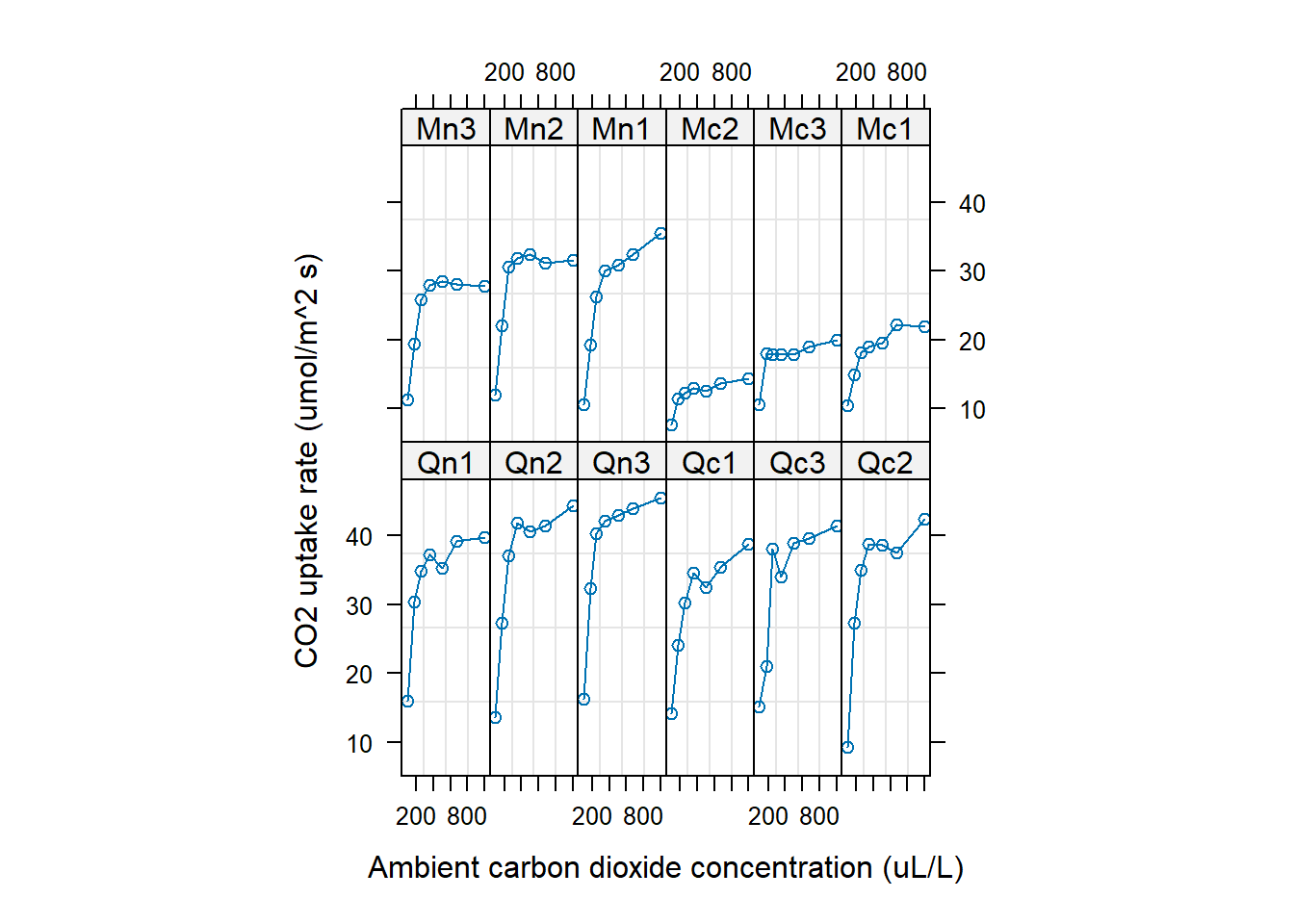
# 相関と回帰 ```{r, setup, include=FALSE, echo=FALSE} :: opts_chunk$ set (collapse = TRUE :: p_load (tidyverse)```  ## 相関 `cor` 関数を用います。`cor` 関数は同じ長さのベクター2つを引数に取り、その2つのベクター間の相関係数を計算する関数です。`cor` 関数の引数にデータフレームを与えると、各行の値の総当りの相関係数(相関行列)を返します。`cor` 関数は通常ピアソンの相関係数を計算する関数ですが、`method="kendall"` や`method="spearman"` を指定するとケンドールの相関係数やスピアマンの相関係数(いずれもノンパラメトリックな相関係数計算の手法)を計算することができます。2つの変数が正規分布しない場合や、直線的な関係にない時(例えば反比例するような場合)にはノンパラメトリックな方法を用いる方がよいときもあります。`cor.test` 関数です。ただし、データ数が多ければ相関係数が0に近くても`cor.test` では統計的に有意となりやすくなります。`GGally` パッケージ[ @GGally_bib ] の`ggpairs` 関数を用いれば、相関係数、`cor.test` の結果、散布図を一度に確認することができます。```{r, filename="相関係数の計算"} # 2変量の相関(ピアソンの相関係数) cor (iris$ Sepal.Length, iris$ Sepal.Width)# ケンドールの相関係数 cor (iris$ Sepal.Length, iris$ Sepal.Width, method= "kendall" )# スピアマンの相関係数 cor (iris$ Sepal.Length, iris$ Sepal.Width, method= "spearman" )# データフレームを引数にした場合の相関行列の計算 cor (iris[, 1 : 4 ])# 相関係数が0ではないことに関する検定 cor.test (iris$ Sepal.Length, iris$ Sepal.Width)# GGally::ggpairsで相関係数等を一度に表示する :: ggpairs (iris[, 1 : 4 ])``` ## 相関係数の大きさと相関の強さ ```{r, echo=FALSE, fig.width=10} set.seed (0 )= runif (100 , - 1 , 1 )= x= x + rnorm (100 , 0 , 0.5 )= x + rnorm (100 , 0 , 0.8 )= x + rnorm (100 , 0 , 3 )= x + rnorm (100 , 0 , 10 )= - x= - x + rnorm (100 , 0 , 0.5 )= - x + rnorm (100 , 0 , 0.8 )= - x + rnorm (100 , 0 , 3 )= - x + rnorm (100 , 0 , 10 )<- data.frame (x = x, y = c (y1, y2, y3, y4, y5, y6, y7, y8, y9, y10),yl = rep (c ("y1" , "y2" , "y3" , "y4" , "y5" , "y6" , "y7" , "y8" , "y9" , "y10" ), rep (100 , 10 )) |> factor (levels= c ("y1" , "y2" , "y3" , "y4" , "y5" , "y6" , "y7" , "y8" , "y9" , "y10" ))<- d |> group_by (yl) |> summarise (v_col= cor (x, y)) |> _$ v_col |> round (digits= 3 )<- paste0 ("r = " , cor_v)$ colv <- rep (cor_v, rep (100 , 10 )) |> factor (levels= cor_v)|> ggplot (aes (x= x, y= y, color= yl))+ geom_point (size= 1 )+ facet_wrap (~ colv, nrow= 2 , scales= "free_y" )+ theme (legend.position= "none" )``` [ @anscombe1973graphs ] 。Rでは`anscombe` のデータセットとして利用できます。このデータセットでは、`x1` と`y1` 、`x2` と`y2` 、`x3` と`y3` 、`x4` と`y4` のそれぞれの列間の相関が一致します。```{r, filename="Anscombeのデータ"} ``` ```{r, filename="Anscombeのデータの相関係数"} <- data.frame (cor_set = rep (c ("x1" , "x2" , "x3" , "x4" ), rep (11 , 4 )),x = anscombe[,1 : 4 ] |> unlist (),y = anscombe[,5 : 8 ] |> unlist ()|> group_by (cor_set) |> summarise (corcoef = cor (x, y))``` ```{r, filename="Anscombeのデータをグラフとして表示する"} |> ggplot (aes (x = x, y = y, color = cor_set)) + geom_point (size = 2 ) + geom_smooth (method = "lm" , se = FALSE ) + facet_wrap (~ cor_set)``` ## 回帰 ## 線形回帰:単回帰 ## ggplot2のコード ```{r, eval=FALSE} set.seed (0 )<- rnorm (50 , mean = 10 , sd = 2 )<- 0.5 * x + 3 + rnorm (50 )<- lm (y ~ x)<- predict (lmresult)<- data.frame (x, y, pred)|> ggplot (aes (x = x, y = y, ymax = pred, ymin = y))+ geom_linerange (linewidth = 1 , color = "#F8766D" )+ geom_point (size = 3 , color = "#00BFC4" )+ geom_abline (intercept = lmresult$ coefficients[1 ], slope = lmresult$ coefficients[2 ], color = "black" , linewidth = 0.25 )+ labs (title = "最小二乗法のイメージ" , caption = "青点:データの点、黒線:線形回帰の線、赤線:最小二乗法で最小とする長さ" )``` ```{r, echo=FALSE} set.seed (0 )<- rnorm (50 , mean = 10 , sd = 2 )<- 0.5 * x + 3 + rnorm (50 )<- lm (y ~ x)<- predict (lmresult)<- data.frame (x, y, pred)|> ggplot (aes (x = x, y = y, ymax = pred, ymin = y))+ geom_linerange (linewidth = 1 , color = "#F8766D" )+ geom_point (size = 3 , color = "#00BFC4" )+ geom_abline (intercept = lmresult$ coefficients[1 ], slope = lmresult$ coefficients[2 ], color = "black" , linewidth = 0.25 )+ labs (title = "最小二乗法のイメージ" , caption = "青点:データの点、黒線:線形回帰の線、赤線:最小二乗法で最小とする長さ" )``` `lm` 関数を用います。`lm` 関数の引数はformulaで、`目的変数~説明変数` という形で、チルダ(`~` )の前に結果(目的変数)のデータ、チルダの後に原因(説明変数)のデータをつないで用います。`lm` 関数の結果として、coefficients(係数、パラメータ)が2つ求まります。1つはIntercept、つまり切片で、もう一つは説明変数に対する傾きです。下の例では、$Sepal.Length = 6.5262 - 0.2234 \cdot Sepal.Width$という線形で回帰の式が表されることを示しています。```{r, filename="線形回帰(単回帰)"} <- iris |> filter (Species == "setosa" )lm (iris_se$ Sepal.Length ~ iris_se$ Sepal.Width)``` `lm` 関数では、`t.test` 関数([ 29章 ](chapter29.qmd#t検定) 参照)と同様に`data` 引数にデータフレームを取り、formulaにはデータフレームの列名を用いることができます。```{r, filename="data引数"} head (cars)lm (dist ~ speed, data = cars)``` `lm` 関数で切片を0、つまり原点を通る線で回帰したい場合には、formulaに`+0` や`-1` を加えます。```{r, filename="切片0の回帰"} lm (dist ~ speed + 0 , data = cars)lm (dist ~ speed - 1 , data = cars) # 上と同じ ``` ### lmクラスのオブジェクトの取り扱い `$coefficients` で切片と傾きを取り出すことができます。また、`summary` 関数の引数とすると、回帰の詳細が表示されます。`summary` 関数で示される回帰の詳細には、coefficientsとして、分散分析表のようなものが表示されます。この表のうち、Estimateは切片と傾きの推定値、Std. Errorは切片と傾きの標準誤差、t valueとPr(>|t|)はt検定の結果を示しています。このt検定の結果は、coefficients(切片と傾き)が0と有意に異なっているかを示しています。以下の例では、Intercept、iris_se\$Sepal.Widthは0と有意に異なります。つまり、`Sepal.Width` は目的変数である`Sepal.Length` に影響を与えていることを表しています。```{r, filename="lmクラスの取り扱い"} <- lm (iris_se$ Sepal.Length ~ iris_se$ Sepal.Width) # 変数にlmの結果を代入 class (lmresult) # lmクラスのオブジェクト $ coefficients # 切片と傾きを取り出す summary (lmresult) # 線形回帰の詳細(内容の詳細は?summary.lmで調べることができる) ``` ### predict関数 `predict` 関数は、lmクラスのオブジェクトを引数に取り、xの値を与えた時のyの値や、yの信頼区間を計算する関数です。`predict` 関数の第一引数はlmクラスのオブジェクトで、第二引数(`newdata` )に、予測したいx軸上の値をデータフレームで設定します。`interval` という引数には、`"none"` 、`"confidence"` 、`"prediction"` の3つのうちどれかを設定します。`"none"` の場合には`newdata` で与えたxを与えた場合の直線上のyの値のみを返します。`"confidence"` の場合は信頼区間、`"prediction"` の場合は個々の値に関する予測区間が表示されます。区間の幅は`levels` 引数で指定することができます。`levels` 引数のデフォルト値は0.95なので、`levels` を設定しない場合には信頼区間などの区間は95%区間として求まります。```{r, filename="データの準備"} set.seed (0 )<- rnorm (15 ) # xは平均0、標準偏差1の正規乱数 <- x + rnorm (15 ) # yはxに正規乱数を足したもの plot (x, y, xlim = c (- 1.75 , 2.5 ), ylim = c (- 2 , 2.5 ))par (new = T)plot (\(x){x}, xlim = c (- 1.75 , 2.5 ), ylim = c (- 2 , 2.5 ), xlab = "" , ylab = "" )``` ```{r, filename="predict関数の利用"} <- lm (y ~ x)<- data.frame (x = 1 : 5 ) # x=1~5のときの予測値を求める # fitが直線上の値、lwr、uprがそれぞれ信頼区間の2.5%、97.5%分位値 predict (lmr, newdata = new, interval = "confidence" , levels = 0.95 )``` ```{r, filename="95%信頼区間を加えた回帰のグラフ"} # predict関数を用いて表示する方法。geom_smooth関数でも同じことができる。 ggplot ()+ geom_point (data = data.frame (x, y), aes (x = x, y = y, size = 2 )) + geom_ribbon (data = data.frame (x = seq (- 2 , 2.5 , by = 0.1 ), predict (lmr, newdata = data.frame (x = seq (- 2 , 2.5 , by = 0.1 )), interval = "confidence" , levels = 0.95 )),aes (x = x, y = fit, ymax = upr, ymin = lwr, color = factor (1 ), fill = factor (1 ), alpha = 0.2 )``` ## lmオブジェクトを引数とする関数について `predict` 関数、`summary` 関数以外にも、`lm` 関数の結果(lmクラスのオブジェクト)にはいろいろな取り扱いの方法があります。まずは、`names` 関数の引数にすると、パラメータの取り出しに用いる名前を呼び出すことができます。```{r, filename="lmクラスのオブジェクトをnames関数の引数に取る"} names (lmr)``` `plot` 関数の引数に取ると、残差(residuals)の分析に関する図を表示することができます。```{r, filename="plot関数:残差プロットの表示", fig.height=8, fig.width=6} # 上の2つは分散の正規性、左下は分散の一様性、 # 右下はCook's distance (https://en.wikipedia.org/wiki/Cook%27s_distance)と呼ばれる # パラメータを示す図で、0.5の点線を超える点は回帰に大きな影響を与えることを示す par (mfrow = c (2 , 2 ))plot (lmr)``` `coef` 関数でcoefficients(切片と傾き)、`confint` 関数で切片と傾きの信頼区間、`residuals` 関数で残差を求めることができます。詳しくは`?lm` のヘルプを参照してください。```{r, filename="パラメータを演算するための関数"} coef (lmr) # 切片と傾きの推定値 confint (lmr) # 切片と傾きの95%信頼区間 residuals (lmr) # 残差 ``` ## 重回帰 `lm` 関数で計算することができます。重回帰は[ 二元分散分析 ](chapter29.qmd#二元分散分析) と同様に、説明変数を`+` または`*` でつないでformulaを設定します。`+` でつないだ場合には交互作用なし、`*` でつないだ場合には交互作用ありの重回帰となります。ただし、重回帰の交互作用はその意味の理解が難しいため、意味をよく考えた上で交互作用の項を追加するかどうか決める方がよいでしょう。```{r, filename="lm関数で重回帰"} # 交互作用なしモデル # Sepal.Length = 2.3037 + 0.6674 * Sepal.Width + 0.2834 * Petal.Length が結果となる lm (iris_se$ Sepal.Length ~ iris_se$ Sepal.Width + iris_se$ Petal.Length)# 交互作用ありモデル # Sepal.Length = -1.3686 + 1.7230 * Sepal.Width + # 2.8759 * Petal.Length - 0.7438 * Sepal.Width * Petal.Length lm (iris_se$ Sepal.Length ~ iris_se$ Sepal.Width * iris_se$ Petal.Length)# 交互作用はコロン(:)を用いて以下のように書くこともできる lm ($ Sepal.Length ~ $ Sepal.Width + iris_se$ Petal.Length + iris_se$ Sepal.Width: iris_se$ Petal.Length``` ## 一般線形モデル [ 共分散分析 ](chapter29.qmd#共分散分析) の拡張だと考えるとよいかと思います。Rでは一般線形モデルの計算も`lm` 関数を用いて行います。一般線形モデルも重回帰とほぼ同じで、説明変数同士を`+` か`*` でつなぐだけです。`:` (コロン)を用いるとよいでしょう。```{r, filename="一般線形モデル"} # 一般線形モデル # 結果は Sepal.Length = 2.39039 + 0.43222 * Sepal.Width + 0.77563 * Petal.Length で、 # 種がsetosaなら上記の線形式のまま、versicolorなら-0.95581、virginicaなら-1.39410を線形式に足す形となる。 lm (iris$ Sepal.Length ~ iris$ Sepal.Width + iris$ Petal.Length + iris$ Species) |> summary ()``` ```{r, filename="交互作用ありの一般線形モデル"} # 一般線形モデル(交互作用あり):たくさんの交互作用項が出てくる lm (iris$ Sepal.Length ~ iris$ Sepal.Width * iris$ Petal.Length * iris$ Species) |> summary ()``` ## formulaの様々な設定方法 [ 29章 ](chapter29.qmd#formulaを用いたt検定) で簡単に説明した通り、formulaは`formula` 関数を用いて文字列から作成することができます。交互作用のある場合も同様です。```{r, filename="formula関数"} formula ("x ~ f" )``` ```{r, filename=".を用いて説明変数を設定する"} # Sepal.Width、Petal.Length、Speciesが説明変数となる lm (Sepal.Length ~ ., data = iris) |> coef ()``` `(.)^2` という形で書くこともできます。```{r, filename="すべての交互作用を評価する"} lm (Sepal.Length ~ (.)^ 2 , data = iris) |> coef ()``` `(x1 + x2)^2` のように設定することもできます。```{r, filename="一部の交互作用のみ評価する"} # Sepal.WidthとPetal.Lengthの交互作用のみ評価する lm (Sepal.Length ~ (Sepal.Width + Petal.Length)^ 2 + Petal.Width, data = iris) |> coef ()``` `I` 関数を用いたformulaを設定します。`I` 関数を用いないと正しい結果が返ってきません。```{r, filename="I関数を用いて多項式回帰を行う"} # Sepal.Widthの2乗のパラメータを評価する lm (Sepal.Length ~ Sepal.Width + I (Sepal.Width^ 2 ), data = iris) |> coef ()``` `?formula` を実行し、`formula` 関数のヘルプを確認してみるとよいでしょう。## 一般化線形モデル ## 二項分布 :1と未回復: 0の2値)を回帰する場合などが挙げられます。```{r} set.seed (5 )<- \(x, sex){1 / (1 + exp (- 3 * x + 150 + 10 * sex)) + rbeta (length (x), 0.5 , 1.5 )}<- 1 : 100 ; sex <- rbinom (100 , 1 , 0.5 )<- data.frame (x, y = if_else (logistic (x, sex) > 0.5 , 1 , 0 ), sex = factor (sex))|> ggplot (aes (x = x, y = y, color = sex)) + geom_point ()``` ## 2項分布を直線で回帰 ```{r, warnings=FALSE, message=FALSE} |> ggplot (aes (x = x, y = y, color = sex)) + geom_point () + geom_quantile (quantiles = 0.5 )) |> print () |> suppressWarnings ()``` ## ポアソン分布 ```{r} <- 1 : 10 <- c (replicate (10 , rpois (10 , exp (x / 3 + 0.25 ))), replicate (10 , rpois (10 , exp (x / 3 ))))<- data.frame (x, y = as.vector (y), fertilizer = factor (rep (c (1 , 0 ), c (100 , 100 ))))|> ggplot (aes (x = x, y = y, color = fertilizer)) + geom_jitter (width = 0.1 )``` ## ポアソン分布を直線回帰 ```{r, warnings=FALSE, message=FALSE} |> ggplot (aes (x = x, y = y, color = fertilizer)) + geom_jitter (width = 0.1 ) + geom_quantile (quantiles = 0.5 )``` ## 尤度と最尤法 [ 28章 ](./chapter28.html) で示した正規分布の確率密度関数です。\| )になっているところです。この縦線の左は自由な値を取ることができる変数(未知の値、上の式ではx)、縦線の右はあらかじめわかっている数値(既知の値、上の式ではμとσ)を表します。ですので、上の式の意味は、平均値(μ)と標準偏差(σ)がわかっているときの、xという値が得られる確率(密度)を計算している、ということを意味しています。\| の左右が逆になっているだけです。ただし、通常データは複数取れる(x~1~~x~n~)ので、μとσが得られる確率は以下のように、データの数だけ尤度を掛け算することで計算できます。## リンク関数 ```{r, echo=FALSE} data.frame (` 目的変数の分布 ` = c ("二項分布" , "正規分布" , "ガンマ分布" , "逆ガウス分布" , "ポアソン分布" , "疑似二項分布" , "疑似ポアソン分布" ),` リンク関数 ` = c ("logit" , "identity" , "inverse" , "1/mu^{2}" , "log" , "logit" , "log" ),` 回帰する関数 ` = c ("ロジスティック" , "直線" , "反比例" , "(1/(ax+b))^0.5" , "指数" , "ロジスティック" , "指数" )|> :: kable ()``` ### 目的変数が正規分布の場合 `glm` 関数で行います。`glm` 関数の使い方は`lm` 関数とほぼ同じで、第一引数に`目的変数~説明変数` の形のformulaを取ります。データフレームのデータを利用する場合には、`data` 引数にデータフレームを指定します。また、`glm` では、目的変数の分布を`family` 引数に指定します。目的変数が正規分布する場合には、以下のように`family="gaussian"` と指定します。`family="gaussian"` の場合、`glm` での回帰の結果は`lm` での回帰の結果と同一になります。```{r, filename="glm関数:正規分布"} ## 一般化線形モデル # 正規分布(identityをリンク関数とする) # lmと同じなので、結果は Sepal.Length = 6.5262 - 0.2234 * Sepal.Width となる glm (Sepal.Length ~ Sepal.Width, data = iris, family = "gaussian" )``` `glm` 関数の返り値を`summary` 関数の引数とすることで、`lm` 関数と同様に詳細な計算結果を得ることができます。Estimateが係数であることは`lm` 関数と同じです。```{r, filename="glm関数:summaryで詳細を調べる"} glm (Sepal.Length ~ Sepal.Width, data = iris, family = "gaussian" ) |> summary ()``` ### 目的変数が二項分布の場合 `glm` の引数に`family="binomial"` (二項分布)を指定します。`family` に二項分布を指定すると、リンク関数はロジットとなり、ロジスティック式でデータを回帰することになります。ロジスティック式が表しているのは確率になるため、説明変数に応じてベルヌーイ試行の確率がどのように変化していくのかを示すような回帰を行うことになります。```{r, filename="glm関数:二項分布"} # 回帰するデータ plot (binom_d$ x, binom_d$ y, xlim = c (0 , 100 ), ylim = c (0 , 1 ))# 二項分布(logitをリンク関数とする) glm (y ~ x, data = binom_d, family = "binomial" )# 回帰の結果をプロットする par (new = T)plot (\(x)(1 / (1 + exp (- (- 4.34896 + 0.09368 * x)))), xlim = c (0 , 100 ), ylim = c (0 , 1 ), xlab = "" , ylab = "" )``` ```{r, echo=FALSE} <- 1 : 10 <- 1 / (1 + exp (- (x - 5 )))<- numeric (10 )for (i in 1 : 10 ){<- rbinom (10 , 1 , prob = probs[i]) |> sum ()<- 10 - y<- data.frame (x, y, z)``` `~` )の左側に、`cbind(成功回数, 失敗回数)` の形で行列として指定します。```{r, filename="cbindで二項分布の成功・失敗を指定"} # yはベルヌーイ試行の成功数、zは失敗数 head (dbn)# 成功・失敗をmatrixで指定する glm (cbind (y, z) ~ x, family = "binomial" )# 回帰をグラフで表示 |> ggplot (aes (x = x, y = y / 10 ))+ geom_point ()+ geom_function (fun= \(x){1 / (1 + exp (- (- 5.025 + 1.119 * x)))})``` #### 説明変数を増やす `lm` 関数と同様に、`formula` の右辺に`+` で説明変数を繋ぐことで、重回帰・一般線形モデルのように説明変数を増やすこともできます。```{r, filename="glm関数:二項分布で説明変数を増やす"} head (binom_d)# 二項分布(logitをリンク関数とする) glm (y ~ x + sex, data = binom_d, family = "binomial" )# 回帰の結果をプロットする |> ggplot (aes (x = x, y = y, color = sex))+ geom_point ()+ geom_function (fun = \(x){1 / (1 + exp (- (- 4.20991 + 0.09672 * x)))}, color = "blue" ) + geom_function (fun = \(x){1 / (1 + exp (- (- 4.20991 - 0.52864 + 0.09672 * x)))}, color = "red" )``` ### 目的変数がポアソン分布の場合 `glm` 関数の`family` 引数を、`family = "poisson"` の形で指定します。```{r, filename="glm関数:ポアソン分布"} head (pois_d)glm (y ~ x, data = pois_d, family = "poisson" )plot (pois_d$ x, pois_d$ y, xlim = c (0 , 10 ), ylim = c (0 , 50 ))par (new = T)plot (\(x){exp (0.1510 + 0.3331 * x)}, xlim = c (0 , 10 ), ylim = c (0 , 50 ), xlab = "" , ylab = "" )``` `+` でつなぐことで、重回帰のように説明変数を増やすことができます。```{r, filename="glm関数:ポアソン分布で説明変数を増やす"} glm (y ~ x + fertilizer, data = pois_d, family = "poisson" )|> ggplot (aes (x = x, y = y, color = fertilizer))+ geom_point ()+ geom_function (fun = \(x){exp (0.03425 + 0.33310 * x)}, color = "red" )+ geom_function (fun = \(x){exp (0.03425 + 0.22131 + 0.33310 * x)}, color = "blue" )``` ## 線形混合モデル  [ `nlme`パッケージ ](https://cran.r-project.org/web/packages/nlme/index.html) [ @nlme_bib; @nlme_book ] 、[ `lme4`パッケージ ](https://cran.r-project.org/web/packages/lme4/index.html) [ @lme4_bib ] 、[ `lmerTest`パッケージ ](https://cran.r-project.org/web/packages/lmerTest/index.html) [ @lmerTest_bib ] のいずれかを使うのが一般的です。`lme4` は`nlme` の改良版、`lmerTest` は`lme4` に分散分析の計算方法を追加したパッケージです。どれを用いても大きな差はありませんが、`lme4` と`lmerTest` が使われているのをよく見る印象があります。`lme4` パッケージに登録されている`sleepstudy` を用います。この`sleepstudy` は睡眠をとっていない被験者の反応時間を毎日取得したデータです。睡眠をとらない期間が延びると、反応時間が延びていく様子が記録されていますが、被験者ごとに傾きも切片も異なる、ランダム切片+ランダム傾きを持つように見えるデータとなっています。```{r, filename="sleepstudyのデータ"} # 線形混合モデルのデータ :: p_load (lmerTest)data ("sleepstudy" , package = "lme4" )head (sleepstudy)# DaysとReactionの関係を調べる ggplot (sleepstudy, aes (x = Days, y = Reaction, color = Subject, alpha = 0.5 )) + geom_point (size = 2 ) + theme (legend.position = "none" ) + geom_line ()``` ### ランダム切片モデル `lmerTest` パッケージ(もしくは`lme4` パッケージ)の`lmer` 関数を用います。`lmer` 関数の使い方は`lm` 関数とほぼ同じですが、ランダム切片とランダム傾きの項をformulaで表す必要があります。formulaは`目的変数+説明変数+(ランダム傾き|ランダム切片)` という形で設定し、縦線(`|` )の左にランダム傾き、右にランダム切片の項を入力します。ランダム切片のみの場合には`目的変数+説明変数+(1|ランダム切片)` という形で、ランダム傾きの部分に1を入れます。```{r, filename="lmer関数でランダム切片モデルを計算"} <- lmer (Reaction ~ Days + (1 | Subject), data = sleepstudy)%>% summary ()``` ### ランダム傾きモデル `sleepstudy` の場合では、`Days` の方向にランダムな傾きが生じるため、ランダム傾きの項に`Days` を指定して計算します。```{r, filename="lmer関数でランダム傾きモデルを計算"} lmer (Reaction ~ Days + (Days | Subject), sleepstudy) %>% summary ()``` ### 線形回帰と線形混合モデルの比較 ```{r, filename="線形回帰、ランダム切片モデル、ランダム傾きモデルの比較"} <- lm (Reaction ~ Days, data = sleepstudy) # 線形モデル <- lmer (Reaction ~ Days + (1 | Subject), data = sleepstudy) # ランダム切片モデル <- lmer (Reaction ~ Days + (Days | Subject), sleepstudy) # ランダム傾きモデル # 固定効果はすべて同じ $ coefficients@ beta@ beta``` ```{r, filename="固定効果の信頼区間"} <- data.frame (Days = seq (0 , 9 , by = 0.1 ), Subject = 308 )<- data.frame (predict (lm_sleepstudy, d, interval = "confidence" ))<- data.frame (Days = sleepstudy$ Days,predict (llm_ri_sleepstudy, re.form = NA , se.fit = TRUE , allow.new.levels = TRUE ))<- data.frame (Days = sleepstudy$ Days,predict (llm_rs_sleepstudy, re.form = NA , se.fit = TRUE , allow.new.levels = TRUE ))<- ggplot () + geom_ribbon (aes (x = Days, ymax = upr, ymin = lwr), data = lm_ci, color = 1 , fill = 1 ) + labs (title = "線形回帰" )<- ggplot () + geom_ribbon (aes (x = Days, ymax = fit + se.fit, ymin = fit - se.fit), data = llm_ri_ci[1 : 10 , ], color = 2 , fill = 2 ) + labs (title = "ランダム切片モデル" )<- ggplot () + geom_ribbon (aes (x = Days, ymax = fit + se.fit, ymin = fit - se.fit), data = llm_rs_ci[1 : 10 , ], color = 3 , fill = 3 ) + labs (title = "ランダム傾きモデル" )library (patchwork)+ p2 + p3``` ### coef関数で個別の傾き・切片を求める `coef` 関数を用いて個別の被験者の傾き・切片を求めることができます。線形混合モデルでは、この個別の被験者の傾き・切片を演算するときに、固定効果、つまり他の被験者のデータを「借りて」傾き・切片を計算することで、より正確に個別被験者の傾き・切片を求めることができます。`coef` 関数の返り値に表れています。```{r, filename="coef関数を用いて個別の被験者の傾き・切片を求める"} # ランダム切片モデル coef (llm_ri_sleepstudy)$ Subject |> head () # Days(傾き)が一定 # ランダム傾きモデル coef (llm_rs_sleepstudy)$ Subject |> head () # Days(傾き)が個々に異なる ``` ## lmer関数の返り値の取り扱い方 `lmerTest::lmer` 関数の返り値はS4オブジェクトなので、`@` や`$` を用いて計算結果にアクセスすることができます。また、`coef` 関数のような関数(アクセサ)を用いて計算結果にアクセスすることもできます。```{r} <- lmer (Reaction ~ Days + (Days | Subject), sleepstudy)@ sigma # 残差の標準偏差 anova (result_lmer, type = "I" ) # type Iの分散分析結果 ``` ## 一般化線形混合モデル `lme4` パッケージの`glmer` 関数で計算することができます。`glmer` 関数は`lmer` 関数と同じく`lme4` パッケージの関数ですので、`glmer` 関数の使い方は基本的に`lmer` 関数と同じです。`lme4` パッケージに含まれる`cbpp` ([ 牛肺疫 ](https://ja.wikipedia.org/wiki/%E7%89%9B%E8%82%BA%E7%96%AB) にかかった牛のデータ)での計算例を以下に示します。```{r, filename="cbppの内容"} # cbpp(contagious bovine pleuropneumonia、牛肺疫)に関するデータ data (cbpp, package = "lme4" ) # herdは牛の群、incidenceは牛肺疫への罹患数、sizeは群内の牛の数、periodは観察時期 head (cbpp) |> ggplot (aes (x = period |> as.character () |> as.numeric (), y = incidence / size, color = herd)) + geom_point () + geom_line ()``` `glmer` の引数の指定は、`glm` と`lmer` を合わせたような形になります。ですので、`family` 引数に目的変数の分布を指定し、ランダム切片、ランダム傾きは、formulaに`(ランダム傾き|ランダム切片)` の形で指定します。演算結果はFixed effectsに示された通り、以下の式となります。```{r, filename="glmer関数で一般化線形混合モデルを計算"} cbind (cbpp$ incidence, cbpp$ size - cbpp$ incidence) |> head () # 左が牛肺疫に罹患した牛、右は罹患していない牛 # 一般化線形混合モデル(ランダム切片) glmer (cbind (incidence, size - incidence) ~ period |> as.numeric () + (1 | herd), family = "binomial" , data = cbpp)``` `lme4` パッケージの他に、RではGLMMの計算に関わるパッケージとして、[ `glmm` ](https://cran.r-project.org/web/packages/glmm/index.html) [ @glmm_bib ] や[ `MCMCglmm` ](https://cran.r-project.org/web/packages/MCMCglmm/index.html) [ @MCMCglmm_bib ] などがあります。一般化線形モデル・一般化線形混合モデルについて詳しく知りたい方は[ データ解析のための統計モデリング入門 ](https://www.amazon.co.jp/%E3%83%87%E3%83%BC%E3%82%BF%E8%A7%A3%E6%9E%90%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AE%E7%B5%B1%E8%A8%88%E3%83%A2%E3%83%87%E3%83%AA%E3%83%B3%E3%82%B0%E5%85%A5%E9%96%80%E2%80%95%E2%80%95%E4%B8%80%E8%88%AC%E5%8C%96%E7%B7%9A%E5%BD%A2%E3%83%A2%E3%83%87%E3%83%AB%E3%83%BB%E9%9A%8E%E5%B1%A4%E3%83%99%E3%82%A4%E3%82%BA%E3%83%A2%E3%83%87%E3%83%AB%E3%83%BBMCMC-%E7%A2%BA%E7%8E%87%E3%81%A8%E6%83%85%E5%A0%B1%E3%81%AE%E7%A7%91%E5%AD%A6-%E4%B9%85%E4%BF%9D-%E6%8B%93%E5%BC%A5/dp/400006973X/ref=sr_1_2?crid=2YDRTUCPZM4HJ&dib=eyJ2IjoiMSJ9.cLlyysXZ_iLOvRYhmMJO8JrLu9tI7C8BlfM7l-0RNeVcFhLjF1qiYu15YvB-rT3Lrpa8oFEXcgLjWYGoh0zZkiPv9d5OFqty6iHTINEyi_6ufuJ_m6rRoH5wQ7TGJFAN651BEnLDZSDbd00hNfVQe6E6exjz-me5Pc9uszWcbYM0xrlzNDIJLfKjaDW54iHjw0crxJ2958tU_HIWu8CyQKgGozQCr5-qa18BMNosh4lsn-4zDcwPLFxvELOeJV8Wl5Spd9jMCTr1kH-fLzwap-WclLOmTVanOXxEYKktzUo.AC94qccYjYbiT6GFuTJIqo4x3g9GOmWkp_8PFHe2fec&dib_tag=se&keywords=%E7%B5%B1%E8%A8%88%E3%83%A2%E3%83%87%E3%83%AA%E3%83%B3%E3%82%B0&qid=1727527212&sprefix=toukeimoderin%2Caps%2C173&sr=8-2) をご一読されるのが良いでしょう。## ベイズモデル ## ベイズの定理 ```{r, echo = FALSE} :: p_load (gplots)<- rep (c ("a" , "b" , "c" ), c (10 , 5 , 5 ))<- rep (c ("a" , "b" , "d" ), c (10 , 5 , 5 ))venn (list (A, B), small = 0 , simplify = TRUE )``` [ RとStanではじめる ベイズ統計モデリングによるデータ分析入門 ](https://www.amazon.co.jp/%E5%AE%9F%E8%B7%B5Data-Science%E3%82%B7%E3%83%AA%E3%83%BC%E3%82%BA-R%E3%81%A8Stan%E3%81%A7%E3%81%AF%E3%81%98%E3%82%81%E3%82%8B-%E3%83%99%E3%82%A4%E3%82%BA%E7%B5%B1%E8%A8%88%E3%83%A2%E3%83%87%E3%83%AA%E3%83%B3%E3%82%B0%E3%81%AB%E3%82%88%E3%82%8B%E3%83%87%E3%83%BC%E3%82%BF%E5%88%86%E6%9E%90%E5%85%A5%E9%96%80-%E9%A6%AC%E5%A0%B4/dp/4065165369/ref=sr_1_9?crid=20JO6XKOMB6C6&dib=eyJ2IjoiMSJ9.ccSkcwrrFMGkM6w1Nb-wbu8EfVftH3K7zLvCgdrJYRC2N0YErf1EkcI9wTaYqCM0axrUblr9PWD-I3v0-RaQRXkK2us7vXdCqh5WW-yDhDj51QhPYPTtliXcb2RLhVXDQWwO7IM1i6VxsVCMGasJccQMmf_K3ss3kzYerpy87qlYPaaM8LK2ug9hwI280LlcEruKWf8MQp56koO4bwPcznWJJLJ9EWiJOa8j9H6m-M_SExCBbYEMS5j2Gt63-4IgzbwVWQEm-Tptv3NIaF9BPdd5r7WsvsvMK7-39DtrS0k.H_18-Puii7nrliRkOeR2uXLZNUTTqmsctKSaMe8CvxA&dib_tag=se&keywords=%E3%83%99%E3%82%A4%E3%82%BA%E7%B5%B1%E8%A8%88&qid=1744457056&sprefix=beizutouke%2Caps%2C173&sr=8-9) や[ StanとRでベイズ統計モデリング ](https://www.amazon.co.jp/Stan%E3%81%A8R%E3%81%A7%E3%83%99%E3%82%A4%E3%82%BA%E7%B5%B1%E8%A8%88%E3%83%A2%E3%83%87%E3%83%AA%E3%83%B3%E3%82%B0-Wonderful-R-%E6%9D%BE%E6%B5%A6-%E5%81%A5%E5%A4%AA%E9%83%8E/dp/4320112423/ref=sr_1_21?crid=20JO6XKOMB6C6&dib=eyJ2IjoiMSJ9.ccSkcwrrFMGkM6w1Nb-wbu8EfVftH3K7zLvCgdrJYRC2N0YErf1EkcI9wTaYqCM0axrUblr9PWD-I3v0-RaQRXkK2us7vXdCqh5WW-yDhDj51QhPYPTtliXcb2RLhVXDQWwO7IM1i6VxsVCMGasJccQMmf_K3ss3kzYerpy87qlYPaaM8LK2ug9hwI280LlcEruKWf8MQp56koO4bwPcznWJJLJ9EWiJOa8j9H6m-M_SExCBbYEMS5j2Gt63-4IgzbwVWQEm-Tptv3NIaF9BPdd5r7WsvsvMK7-39DtrS0k.H_18-Puii7nrliRkOeR2uXLZNUTTqmsctKSaMe8CvxA&dib_tag=se&keywords=%E3%83%99%E3%82%A4%E3%82%BA%E7%B5%B1%E8%A8%88&qid=1744457056&sprefix=beizutouke%2Caps%2C173&sr=8-21) を読むのがよいでしょう。[ 状態空間モデル ](https://logics-of-blue.com/%E7%8A%B6%E6%85%8B%E7%A9%BA%E9%96%93%E3%83%A2%E3%83%87%E3%83%AB%E3%81%A8%E3%81%AF/) というものを利用する場合以外ではベイズモデルを使用することはあまりないと思いますが、ベイズモデルを使って簡単な線形回帰を行うこともできます。[ `brms`パッケージ ](https://paulbuerkner.com/brms/) [ @brms_bib1; @brms_bib2; @brms_bib3 ] を利用するのが良いでしょう。`brms::brm` 関数を用いると、`glm` などと同じように関数を設定し、回帰を行うことができます。`brm` では`prior` 引数に事前分布を設定する必要があります。事前分布の設定がおかしいと計算できない場合もありますので、データを見て慎重に事前分布を定める必要があります。```{r, filename="brmsパッケージでベイズ統計"} # ベイズモデルでの回帰 :: p_load (brms)<- brm (rating ~ period + carry + cs (treat),data = inhaler, family = sratio ("logit" ),prior = set_prior ("normal(0,5)" ), chains = 2 )summary (fit1)# 計算結果をグラフとして表示(ヒストグラムがパラメータの事後分布) plot (fit1, ask = FALSE )``` `brm` 関数は[ Stan ](https://mc-stan.org/) [ @stan_bib ] という乱数計算プログラムに依存しています。さらに複雑なベイズ統計を用いる場合には、[ rstan ](https://cran.r-project.org/web/packages/rstan/index.html) [ @rstan_bib ] や[ CmdStanR ](https://github.com/stan-dev/cmdstanr/tree/master) といったパッケージを利用し、Stanの言語で統計モデルを直接記述し、計算する必要があります。興味がある方には教科書([ データ解析のための統計モデリング入門 ](https://www.amazon.co.jp/%E3%83%87%E3%83%BC%E3%82%BF%E8%A7%A3%E6%9E%90%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AE%E7%B5%B1%E8%A8%88%E3%83%A2%E3%83%87%E3%83%AA%E3%83%B3%E3%82%B0%E5%85%A5%E9%96%80%E2%80%95%E2%80%95%E4%B8%80%E8%88%AC%E5%8C%96%E7%B7%9A%E5%BD%A2%E3%83%A2%E3%83%87%E3%83%AB%E3%83%BB%E9%9A%8E%E5%B1%A4%E3%83%99%E3%82%A4%E3%82%BA%E3%83%A2%E3%83%87%E3%83%AB%E3%83%BBMCMC-%E7%A2%BA%E7%8E%87%E3%81%A8%E6%83%85%E5%A0%B1%E3%81%AE%E7%A7%91%E5%AD%A6-%E4%B9%85%E4%BF%9D-%E6%8B%93%E5%BC%A5/dp/400006973X/ref=sr_1_2?crid=2YDRTUCPZM4HJ&dib=eyJ2IjoiMSJ9.cLlyysXZ_iLOvRYhmMJO8JrLu9tI7C8BlfM7l-0RNeVcFhLjF1qiYu15YvB-rT3Lrpa8oFEXcgLjWYGoh0zZkiPv9d5OFqty6iHTINEyi_6ufuJ_m6rRoH5wQ7TGJFAN651BEnLDZSDbd00hNfVQe6E6exjz-me5Pc9uszWcbYM0xrlzNDIJLfKjaDW54iHjw0crxJ2958tU_HIWu8CyQKgGozQCr5-qa18BMNosh4lsn-4zDcwPLFxvELOeJV8Wl5Spd9jMCTr1kH-fLzwap-WclLOmTVanOXxEYKktzUo.AC94qccYjYbiT6GFuTJIqo4x3g9GOmWkp_8PFHe2fec&dib_tag=se&keywords=%E7%B5%B1%E8%A8%88%E3%83%A2%E3%83%87%E3%83%AA%E3%83%B3%E3%82%B0&qid=1727527212&sprefix=toukeimoderin%2Caps%2C173&sr=8-2) 、[ RとStanではじめる ベイズ統計モデリングによるデータ分析入門 ](https://www.amazon.co.jp/dp/B07WFD5RFS/) や[ StanとRでベイズ統計モデリング ] ((https://www.amazon.co.jp/dp/4320112423/)))を読むことをおススメします。## ガウス過程回帰 [ ベイズ推定する回帰の方法 ](https://www.jstage.jst.go.jp/article/isciesci/62/10/62_390/_pdf) ですので、結果は幅を持った形で推定されます[ @akaho2018 ] 。この手法は回帰ではありますが、上記のようなパラメータを求めて数式が得られるような手法ではなく、主に予測的に用いる方法です。`predict` 関数を用いて、ある説明変数に対する目的変数の値の予測を行う形で用います。`kernlab` パッケージ[ @kernlab_bib1; @kernlab_bib2 ] の`gausspr` 関数を用いて、ガウス過程回帰を計算できます。`gausspr` 関数では説明変数、目的変数に当たる変数をそれぞれ`x` 、`y` 引数に設定して計算します。計算結果は`gausspr` クラスのオブジェクトで、回帰線上の点の位置や標準偏差を求める場合には、`predict` 関数を用いることになります。```{r, filename="ガウス過程回帰"} :: p_load (kernlab)<- seq (- 20 , 20 , 0.1 )<- data.frame (x = x, y = sin (x) / x + rnorm (401 , sd = 0.03 ))plot (d1) # 回帰するデータ # これがガウス過程回帰の計算 <- gausspr (x = d1$ x, y = d1$ y, variance.model = T)# 回帰の結果を見てもよくわからない # xに対する代表値・SDを予測する <- data.frame (x, pred = predict (fit, x))$ sd <- predict (fit, x, type = "sdeviation" ) # 結果をプロット ggplot ()+ geom_point (data = d1, aes (x = x, y = y, color = 1 ), size = 1 ) + geom_ribbon (data = d, aes (x = x, ymax = pred + sd, ymin = pred - sd, color = 2 , fill = 2 ), alpha = 0.5 )+ geom_line (data = d, aes (x = x, y = pred, color = 2 , alpha = 0.5 ), linewidth = 1 )``` ## 説明変数がたくさんある場合の回帰 ## 説明変数の数と過学習  ## 説明変数間の相関と多重共線性 ## AICによるモデル選択 [ @akaike1998information ] です。`glm` 関数を用いると、AICの計算結果を得ることができます。例えば、以下の例では`iris` の`Sepal.Length` を回帰する7つのモデル、説明変数の組み合わせ、のAICを計算しています。AICの結果から、最後のモデル、3つ説明変数があるモデルでAICが最小となる、つまりこの3つ説明変数があるモデルを選択するということになります。```{r, filename="glm関数でAICを求める"} c (glm (Sepal.Length ~ Sepal.Width, data = iris, family = "gaussian" ) |> _$ aic,glm (Sepal.Length ~ Petal.Length, data = iris, family = "gaussian" ) |> _$ aic,glm (Sepal.Length ~ Petal.Width, data = iris, family = "gaussian" ) |> _$ aic,glm (Sepal.Length ~ Sepal.Width + Petal.Length, data = iris, family = "gaussian" ) |> _$ aic,glm (Sepal.Length ~ Petal.Length + Petal.Width, data = iris, family = "gaussian" ) |> _$ aic,glm (Sepal.Length ~ Sepal.Width + Petal.Width, data = iris, family = "gaussian" ) |> _$ aic,glm (Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width, data = iris, family = "gaussian" ) |> _$ aic``` `r options(scipen=100); k <- 0; for(i in 1:20){k <- k + choose(20, i)}; k` 通りと膨大なモデルを比較する必要があります。モデルに交互作用を加えると、更に多くの比較が必要となります。`step` 関数が備わっています。`lm` や`glm` に説明変数をすべて含むformula(**フルモデル**)を設定し、その返り値を`step` 関数の引数とすることで、各モデルのAICを自動的に比較し、AIC最小モデルを選択してくれます。```{r, filename="step関数によるAIC最小モデルの選択"} # 回帰の返り値をlm_irisに代入 <- lm (iris$ Sepal.Length ~ $ Sepal.Width + $ Petal.Length + $ Petal.Width + $ Species)# 下の例ではフルモデル(説明変数をすべて含むモデル)が選択されている # trace = 1とすると、AIC選択の過程が表示される step (lm_iris, trace = 0 ) ``` ## AIC以外の情報量規準 [ WikipediaのModel Selectionのページ ](https://en.wikipedia.org/wiki/Model_selection#Criteria) に記載があります。## スパース回帰 [ glmnetパッケージ ](https://cran.r-project.org/web/packages/glmnet/index.html) [ @glmnet_bib1; @glmnet_bib2; @glmnet_bib3 ] を用います。```{r, filename="ライブラリの読み込み"} ## スパース回帰のライブラリ(mlbenchはデータセットを読み込むためにロード) :: p_load (glmnet, mlbench)``` `BostonHousing` は[ 18章 ](chapter18.qmd#bostonhousing) で説明した通り、1970年国勢調査(センサス)におけるボストンの各地域の住宅価格と、その地域の犯罪率、非小売業の面積の割合、築年数の古い建物の割合、高速道路までのアクセス、税金等を表にしたものです。重回帰の例として、住宅価格をその他のデータで説明する、つまり住宅価格を目的変数、その他のデータを説明変数として用いられることの多いデータです。`BousonHousing` を用いて、AICによるモデル選択とスパース回帰を比較していきます。```{r, filename="BostonHousingのデータ"} data ("BostonHousing" )head (BostonHousing) # データにmlbenchパッケージのBostonHousingを用いる # 前処理 <- BostonHousing$ chas <- as.numeric (tempBoston$ chas)``` ### データの正規化 `scale` 関数を用います。`scale` 関数はベクターもしくはデータフレームを引数に取り、ベクターの場合はそのベクターの平均と標準偏差を、データフレームの場合には列ごとの平均と標準偏差をそれぞれ0、1に変換します。```{r, filename="説明変数の正規化"} # 説明変数になるデータをscale関数で正規化 1 : 13 ] <- tempBoston[1 : 13 ] |> scale ()# 平均が0、標準偏差が1になる 1 : 13 ] |> apply (2 , mean) |> round (digits = 3 )1 : 13 ] |> apply (2 , sd)``` ### AICでモデルを選択する `step` 関数でAICを最小とするモデルの選択を行います。`step` 関数の引数は`lm` 関数や`glm` 関数の返り値ですので、まずは説明変数をすべて使ったフルモデルの`lm` 関数の返り値が必要となります。`+` でつなぐのは大変です。Rでは、formulaの右辺、説明変数の欄に`.` (ピリオド)を入力すると、データフレームのうち、目的変数以外のすべての列を説明変数とすることができます。以下の例では、`BousonHousing` の`medv` (家の価格のデータ)を目的変数、その他の列のデータをすべて説明変数とした`lm` 関数の返り値を`lm_model` に代入しています。`lm_model` を用いて`step` 関数でモデル選択をすると、下記のように切片(intercept)を除いて11個の説明変数の傾きが計算されます。この`step` 関数の計算過程で、`indus` と`age` 、非小売業の面積の割合と築年数の古い建物の割合の項が抜けていることがわかります。```{r, filename="step関数でモデル選択"} colnames (tempBoston) # medvを除くと13列のデータになっている # とりあえずlmとStepでやってみる # 説明変数を.で指定すると、目的変数以外のすべてのデータを説明変数に設定する <- lm (medv ~ ., data = tempBoston)step (lm_model, trace = 0 )``` ### ラッソ回帰 `glmnet` パッケージの`cv.glmnet` 関数です。`cv.glmnet` 関数はformulaを引数に取らず、引数`x` に各列が説明変数である行列、引数`y` に目的変数であるベクターを指定します。さらに、`glm` 関数と同様に目的変数の分布として`family` 引数、ラッソ回帰を指定するための引数である`alpha=1` をそれぞれ指定します。`cv.glmnet` 関数の返り値(下の例では`cvlasso_m` )を`plot` 関数の引数に取ると、Mean-squared error(平均2乗誤差)とラムダの関係を示したグラフが表示されます。このグラフのうち、縦線が引いてある2本のうちラムダの小さい方の値を、正規化項の係数λとして採用します。ですので、下の`BousonHousing` の例では、log(λ)=-3.7付近の値をλとして採用し、ラッソ回帰を行うこととなります。```{r, filename="ラッソ回帰:λを求める"} # ラッソ回帰:正規化項の係数を求める # 乱数計算を含むため、seedを設定しないと計算値は変化する <- cv.glmnet (x = tempBoston[,1 : 13 ] |> as.matrix (), y = tempBoston$ medv, family = "gaussian" , alpha = 1 )# 左側の点線のラムダを採用する plot (cvlasso_m)# 大きい方のlog(λ)の点線の値 $ lambda.1 se |> log () # 小さい方のlog(λ)の点線の値(こちらを採用する) $ lambda.min |> log () ``` `glmnet` 関数で行います。`glmnet` 関数の引数はほぼ`cv.glmnet` 関数と同じです。ラムダを指定せずに`glmnet` 関数での計算を行うと、正規化項の大きさ(L1 norm)やラムダと傾きの関係を求めることができます。この関係を求めるときには、`glmnet` 関数の返り値を`plot` 関数の引数とします。ラムダとの関係を知りたい場合には`plot` 関数の引数に`xvar="lambda"` を追加します。グラフの上に表示される数値は選択される説明変数の数を示しています。lambdaが大きく、L1 normが小さくなるとグラフは0に収束していきますが、これはlambdaとL1 normに従い、傾きが0、つまり説明変数から脱落するものが多くなっていくことを示しています。```{r, filename="ラッソ回帰:傾きの計算1"} # ラッソ回帰:正規化項の係数を入力せずに計算 <- glmnet (x = tempBoston[,1 : 13 ], y = tempBoston$ medv, family = "gaussian" , alpha = 1 )# 正則化項(L1)の大きさと傾き plot (lasso_m)``` `cv.glmnet` 関数でλを計算した値がある場合、`glmnet` 関数の`lambda` 引数に`cv.glmnet` 関数で計算したλの値を指定します。`glmnet` 関数の結果をそのまま見てもよくわかりませんが、返り値はS4オブジェクトとなっており、`$` を用いて情報を取り出すことができます。傾きは`$beta` で呼び出すことができます。```{r, filename="ラッソ回帰:ラムダを指定して傾きの計算"} # ラッソ回帰:正規化項の係数を入力して計算 <- glmnet (x = tempBoston[,1 : 13 ], y = tempBoston$ medv, family = "gaussian" , lambda = cvlasso_m$ lambda.min, alpha = 1 )# モデルと自由度、ラムダ等が帰ってくる # 傾きの項(.は傾き0になっている) $ beta``` `indus` と`age` の結果(s0)が`.` (ピリオド)になっています。この`.` は傾きが0、つまりモデルに組み込まないことを示しています。`step` 関数で落とされた`indus` と`age` がラッソ回帰でも落とされていることがわかります。また、`rm` の傾きが大きく、`lstat` の傾きが小さいことがわかります。`rm` は1住居あたりの部屋数、`lstat` は地位の低い住民の割合ですので、住宅価格は部屋数が増えると高くなり、地位の低い住民の割合が増えると下がる傾向にあることがわかります。### リッジ回帰 `cv.glmnet` 関数でλを計算した上で、`glmnet` 関数で傾きを求めます。ただし、リッジ回帰を行うときには引数`alpha` に`0` を指定します。```{r, filename="リッジ回帰:λを求める"} <- cv.glmnet (x = tempBoston[,1 : 13 ] |> as.matrix (), y = tempBoston$ medv, family = "gaussian" , alpha = 0 )plot (cvridge_m)$ lambda.min %>% log``` ```{r, filename="リッジ回帰:傾きを求める"} <- glmnet (x= tempBoston[,1 : 13 ], y= tempBoston$ medv, family= "gaussian" , lambda= cvridge_m$ lambda.min, alpha= 0 )$ beta``` `cv.glmnet` 関数で計算したラムダを代入して実際に係数を確認すると、ラッソ回帰では.で表示されていた`indus` と`age` も0にはなっておらず、説明変数から外されていないことがわかります。### エラスティックネット `alpha` 引数の値で指定し、`alpha` が1に近いとラッソ寄り、0に近いとリッジ寄りの回帰となります。下の例では`alpha` を0.5としていますが、実際にデータに用いる場合には`alpha` の値を最適化して用います。このように、計算においてある程度自分で最適化が必要となるパラメータのことを機械学習の分野では**ハイパーパラメータ**と呼びます。```{r, filename="エラスティックネット"} # 実際にはアルファを最適化して利用する <- cv.glmnet (x = tempBoston[,1 : 13 ] |> as.matrix (), y = tempBoston$ medv, family = "gaussian" , alpha = 0.5 )plot (cven_m)# ラムダを計算する $ lambda.min %>% log# 計算したラムダを用いて回帰の計算を行う <- glmnet (x = tempBoston[,1 : 13 ], y = tempBoston$ medv, family= "gaussian" , lambda = cven_m$ lambda.min, alpha = 0.5 )$ beta``` ## 主成分回帰 `prcomp` 関数で行います。`prcomp` の返り値は主成分への変換を行うための`prcomp` クラスのオブジェクトで、主成分は`$x` で取り出します。後は`lm` 関数で説明変数に主成分を指定して回帰を行うだけです。`$rotation` でデータを主成分に変換する際の係数が求まります。また、説明変数を主成分に変換する際には`predict` 関数を用います。`predict` 関数の第一引数に`prcomp` オブジェクトを、第二引数に変換したいデータをデータフレームで指定します。計算した主成分を、`lm` オブジェクトを用いた`predict` 関数に与えて予測すれば、主成分回帰による予測値を得ることができます。```{r, filename="主成分回帰"} # 主成分への変換 <- iris[,2 : 4 ] |> prcomp (scale = T)$ x |> head () # 変換後の主成分(PC1~PC3) $ rotation # 主成分への変換の係数 # 目的変数をデータフレームに付け加える <- pc$ x |> as.data.frame ()$ Sepal.Length <- iris$ Sepal.Length# 主成分で回帰(主成分4つをすべて用いる) <- lm (Sepal.Length ~ ., data = pc1)# 予測の例 <- data.frame (Sepal.Width = 5 , Petal.Length = 6 , Petal.Width = 3 )# 予測に用いる説明変数を主成分に変換 <- predict (pc, example_iris)# 主成分を用いて予測値を計算 predict (pcr_lm, pc_example |> as.data.frame ())``` [ `pls`パッケージ ](https://cran.r-project.org/web/packages/pls/index.html) [ @pls_bib ] の`pcr` 関数を用いても行うことができます。```{r, filename="plsパッケージのpcr関数で主成分回帰"} :: p_load (pls)data (yarn)# PCRの計算(ncompは回帰に用いる主成分の数) <- pcr (density ~ NIR, ncomp = 6 , data = yarn, validation = "CV" ) |> summary () # 回帰結果の表示 ``` ## 部分的最小二乗回帰 ### PLS:データの準備とクロスバリデーション `yarn` のデータセットは、PET yarn(ポリエステル糸)の近赤外吸光分光データ(Near Infra Red、[ NIR ](https://ja.wikipedia.org/wiki/%E8%BF%91%E8%B5%A4%E5%A4%96%E7%B7%9A%E5%88%86%E5%85%89%E6%B3%95) )と糸の密度(`density` )の関係を示したデータです。このデータセットでは、予めクロスバリデーション用に`train` という列が追加されており、21行が`TRUE` 、つまり訓練データで、残りの7行が`FALSE` 、つまりテストデータとなっています。```{r, filename="PLSに用いるデータ:yarn"} # yarnはplsパッケージのデータセット :: p_load (pls)data (yarn) # ポリエステル繊維のNIR(近赤外吸収)データ colnames (yarn) # NIRにはNIR.1~NIR.268の列が登録 dim (yarn)summary (yarn$ train) # 21データが訓練、7データがテストデータ ``` [ `pls` ](https://cran.r-project.org/web/packages/pls/index.html) パッケージの`plsr` 関数を用いてPLS回帰を行うことができます。`plsr` 関数の第一引数はformulaです。`ncomp` 引数は回帰に用いる説明変数変換後のパラメータの数で、増やすとデータへの適合度は高くなりますが、過学習のリスクも大きくなります。`validation` には用いるバリデーションの方法を指定します。`validation="CV"` では、`train` の列の論理型を用いてクロスバリデーションを行います。leave-one-outと呼ばれる、データの一つだけをテストデータとして、その他のデータを訓練データとする場合には、`validation="LOO"` と指定します。```{r, filename="部分的最小二乗回帰(PLS)"} <- plsr (~ NIR, ncomp = 6 , data = yarn, validation = "CV" )|> summary ()``` `predict` 関数を用います。`predict` 関数の第一引数に`plsr` 関数の返り値、`comps` 引数には上の`yarn.pls|>summary()` の結果として示されている`comps` のうち、回帰に用いるものを指定します。通常は`plsr` 関数の`ncomp` に指定した数値までのベクターで指定することになります。`newdata` には予測したいデータのデータフレームを指定します。```{r, filename="PLSの結果を用いてデータを予測する"} # モデルにデータを与えてpredictすることで用いる <- predict (comps = 1 : 6 , newdata = yarn[! yarn$ train,])# 左がテストデータ、右が予測値 data.frame (test_data = yarn[! yarn$ train,]$ density, result_prediction) |> :: kable ()``` `density` が正しく予測されているのがわかるかと思います。## ニューラルネットワーク(回帰) [ 次の章 ](chapter31.qmd#ニューラルネットワーク) で説明します。## ニューラルネットワークの仕組み  {width=50%}\{ \begin{align*}Y = 0 \quad (Y \leqq 0) \\ Y = w_{1}a_{1}+w_{2}a_{2}+w_{3}a_{3}+b \quad (Y > 0)\end{align*}\right.$$ [ ゼロから作るDeep Learning ](https://www.amazon.co.jp/dp/4873117585?tag=le2am-22&language=ja_JP)[ @斎藤康毅2016-09-24 ] を読んでみるのがよいでしょう。[ neuralnet ](https://cran.r-project.org/web/packages/neuralnet/index.html) パッケージ[ @neuralnet_bib ] の`neuralnet` 関数を用います。`neuralnet` 関数はformulaを引数に取る関数ですので、まず`iris` のデータを用いてformulaを準備します。formulaの形は`lm` 関数などと同じで、`目的変数~説明変数` の形で準備します。```{r, filename="ニューラルネットワーク:formulaの準備"} :: p_load (neuralnet)<- as.formula ("Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width + Species" ``` `neuralnet` 関数は、この`formula` の他に、`data` 、隠れ層(`hidden` )、活性化関数(`act.fct` )を引数に取ります。隠れ層とは、ニューラルネットワークの中間層のことを指します。以下の式では、隠れ層としてパーセプトロン3つ、3つの2層をベクター(`c(3,3)` )で設定しています。`neuralnet` 関数の返り値を`plot` すると、各入力に対する重みとバイアスを図で表示してくれます。黒の数値が重みで、青の数値はバイアスを示します。```{r, filename="neuralnet関数で2層ニューラルネットワークを計算"} # 2層(nodeが3、3) set.seed (0 )# 説明変数はスケーリングする <- scale (iris[, 2 : 4 ]) |> as.data.frame ()# 種は―1~1にスケーリング $ Species <- iris$ Species |> as.numeric () - 2 # 目的変数は0~1にスケーリング $ Sepal.Length <- $ Sepal.Length - min (iris$ Sepal.Length)) / (max (iris$ Sepal.Length) - min (iris$ Sepal.Length))<- neuralnet (formula = formula_iris,data = iris_scale,hidden = c (3 , 3 ),act.fct = "logistic" , # ソフトマックス(この他に"tanh"を選べる) linear.output = T # 出力層に活性化関数を適用するかどうか plot (nn_iris, rep = "best" )``` `hidden=c(2,3,2)` と隠れ層を設定します。```{r, filename="neuralnet関数で3層ニューラルネットワークを計算"} # 3層(nodeが2、3、2) set.seed (0 )<- neuralnet (formula = formula_iris,data = iris_scale,hidden = c (2 , 3 , 2 ),act.fct = "logistic" , linear.output = Tplot (nn_iris2, rep = "best" )``` `neuralnet` 関数の返り値を`predict` 関数の引数にすることで、予測を行うことができます。ただし、データをあらかじめスケーリングしていること、活性化関数がソフトマックスであることから、計算結果は0~1までの値として得られます。この予測値をうまく変換してやれば、元の値を評価することができます。ただし、下のニューラルネットワークの構造では正確には予測できていないことがわかります。このような場合には、データ変換の方法、隠れ層や活性化関数、その他の引数を最適化する必要があります。```{r, filename="neuralnet関数の返り値で予測"} <- neuralnet (formula = formula_iris,data = iris_scale,hidden = c (4 , 4 ),act.fct = "logistic" , linear.output = T # 上のニューラルネットワークで予測する predict (nn_iris3, iris_scale[1 : 5 ,])# 予測値と実際の値の比較 <- data.frame (# 予測値を変換 prediction = predict (nn_iris3, iris_scale[1 : 50 ,]) * (max (iris$ Sepal.Length) - min (iris$ Sepal.Length)) + min (iris$ Sepal.Length),real_value = iris$ Sepal.Length[1 : 50 ] # 実際の値 plot (pred_real)``` [ nnet ](https://cran.r-project.org/web/packages/nnet/index.html) パッケージ [ @nnet_bib ] があります。## Rでディープニューラルネットワーク [ Tensorflow ](https://www.tensorflow.org/?hl=ja) をRから利用する[ `tensorflow` ](https://tensorflow.rstudio.com/) パッケージ、Tensorflowのニューラルネットワークライブラリである[ Keras ](https://keras.io/) をRから利用する[ `keras` ](https://cran.r-project.org/web/packages/keras/index.html) パッケージ、RからPythonのニューラルネットワークライブラリである[ Pytorch ](https://pytorch.org/) を利用するためのライブラリである[ `torch` ](https://torch.mlverse.org/) などを用いることで、Rでもディープニューラルネットワークを試すことができます。## カーネル密度推定 [ 24章 ](./chapter24.html) で説明した`density` 関数です。`density` 関数の引数にベクターを与えるとカーネル密度を計算してくれます。この`density` 関数の返り値を`plot` 関数の引数にすると、カーネル密度をグラフにしてくれます。[ ggplot2 ](chapter21.qmd#geom_density) の`geom_density` 関数を用いても描画できます。カーネル密度の計算は[ KernSmooth ](https://cran.r-project.org/web/packages/KernSmooth/index.html) パッケージ [ @KernSmooth_bib ] の`bkde` 関数を用いても計算することができます。```{r, filename="カーネル密度推定"} # カーネル回帰 head (faithful)<- faithful$ waitinghist (x, xlim = c (40 , 100 ))par (new = T)density (x) |> plot (xlim = c (40 , 100 ), main = "" , xlab = "" , ylab = "" , axes = FALSE )# KernSmooth::bkde関数を用いる方法 :: p_load (KernSmooth)<- bkde (faithful$ waiting, bandwidth = 3 ) %>% as.data.frameggplot ()+ geom_line (data = est, aes (x = x, y = y* 950 ))+ geom_histogram (data = faithful, aes (x = waiting, fill = 1 ), alpha = 0.5 )+ theme (legend.position = "none" )``` ## 非線形最小二乗法:nls関数 [ ガウス-ニュートン法 ](https://ja.wikipedia.org/wiki/%E3%82%AC%E3%82%A6%E3%82%B9%E3%83%BB%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E6%B3%95) を用いており、[ 局所最適化 ](https://jp.mathworks.com/help/optim/ug/local-vs-global-optima.html) と呼ばれる解にしか到達しない問題が起こることもあります。`nls` 関数です。`nls` 関数は引数に回帰したい関数の数式と各パラメータの初期値、データフレームを取ります。`nls` 関数の使い方は`lm` 関数とよく似ていて、`summary` 関数を用いれば計算結果の詳細を、`predict` 関数を用いれば回帰からの予測を得ることができます。```{r, filename="nls関数で非線形最小二乗法"} <- subset (DNase, Run == 1 )plot (density ~ conc, data = DNase1)# SSlogis関数は初期値を自動設定してくれる(self start)nlsのロジスティック回帰用の関数 <- nls (density ~ SSlogis (log (conc), Asym, xmid, scal), DNase1) # Asymは漸近線を示すパラメータ、xmidは変曲点のx軸の値を示すパラメータ、 # scalはスケールパラメータ summary (fm1DNase1)# predict関数で予測することができる predict (fm1DNase1, data.frame (conc = seq (0 , 12 , by= 0.1 ))) |> head ()# 回帰結果のグラフ <- data.frame (conc = seq (0 , 12 , by= 0.1 ), pred = predict (fm1DNase1, data.frame (conc = seq (0 , 12 , by = 0.1 ))))ggplot ()+ geom_point (data = DNase1, aes (x = conc, y = density, color = "#F8766D" ))+ geom_line (data = d, aes (x = conc, y = pred), color = "#00BFC4" )+ theme (legend.position = "none" )``` ## LOESS・LOWESS平滑化 `loess` 関数でLOESS平滑化、`lowess` 関数を用いてLOWESS平滑化の計算を行います。どちらも同じ計算を行う関数ですが、関数の使い方が少し異なります。`loess` 関数は`loess` オブジェクトを返す関数で、`predict` 関数を用いて予測値を計算する形になっています。また、平滑化の幅を指定する`span` 引数を設定することで、より細かな値の変動に対応した平滑化を行うこともできます。```{r, filename="LOESS平滑化"} <- loess (dist ~ speed, data = cars) # spanのデフォルト値は0.75 summary (loess_cars)<- loess (dist ~ speed, cars, span = 0.3 ) # spanを短く設定 # 赤がspan=0.75、青がspan=0.3 plot (cars, xlim = c (0 , 30 ), ylim = c (0 , 120 ))par (new = T)plot (seq (5 , 30 , by = 0.1 ), predict (loess_cars, data.frame (speed = seq (5 , 30 , by = 0.1 ))), type = "l" , xlim = c (0 , 30 ), ylim = c (0 , 120 ),xlab = "" ,ylab = "" ,col = 2 )par (new = T)plot (seq (5 , 30 , by = 0.1 ), predict (loess_cars2, data.frame (speed = seq (5 , 30 , by = 0.1 ))), type = "l" , xlim = c (0 , 30 ), ylim = c (0 , 120 ),xlab = "" ,ylab = "" ,col = 5 )``` `lowess` 関数は平滑化後の`x` と`y` のセットをリストとして返す関数で、`plot` 関数や`lines` 関数の引数に取ることで平滑化した線を描画することができます。平滑化計算における説明変数側の値の幅は`delta` 引数で指定します。デフォルトでは横軸を100分割して平滑化することになっています。部分最適化の幅を指定する引数が`f` で、`f` に小さい値を指定することで、より細かな値の変動を捉えることができます。`loess` 、`lowess` のどちらを使っても結果自体には大差はありませんが、`loess` 関数の方が予測値の融通が利きやすい仕様になっています。```{r, filename="LOWESS平滑化"} lowess (cars) # 返り値は同じ長さのxとyのリストになる plot (cars, main = "lowess(cars)" )lines (lowess (cars), col = 2 ) # 赤色の線 lines (lowess (cars, f = 0.1 ), col = 5 ) # 部分最適化の幅を狭くする(青色) ``` ## spline回帰 ```{r, echo=FALSE} <- seq (- 10 , 10 , by= 0.05 )<- 3 * x^ 2 <- data.frame (x, y)<- seq (0 , 20 , by= 0.05 )<- - 1.5 * (x2 - 15 )^ 2 + 225 <- data.frame (x2, y2)set.seed (2 )<- data.frame (x = seq (- 10 , 20 , by= 2 ), y = c (3 * seq (- 10 , 5 , by= 2 ) ^ 2 + rnorm (8 , 0 , 25 ),- 1.5 * (seq (5 , 20 , by= 2 ) - 15 )^ 2 + 225 + rnorm (8 , 0 , 25 )plot (d3, xlim= c (- 10 , 20 ), ylim= c (- 112.5 , 300 ),main= "spline平滑化のイメージ" ,cex = 2 ,pch = 19 )par (new= T)plot (|> filter (x <= 5 ) |> _$ x, |> filter (x <= 5 ) |> _$ y, xlim= c (- 10 , 20 ), ylim= c (- 112.5 , 300 ), type= "l" , col= 2 ,lwd= 4 , xlab= "" , ylab= "" )par (new= T)plot (|> filter (x > 5 ) |> _$ x, |> filter (x > 5 ) |> _$ y, xlim= c (- 10 , 20 ), ylim= c (- 112.5 , 300 ), type= "l" , col= 2 ,lwd= 0.5 , xlab= "" , ylab= "" )par (new= T)plot (|> filter (x2 > 5 ) |> _$ x2, |> filter (x2 > 5 ) |> _$ y2, xlim= c (- 10 , 20 ), ylim= c (- 112.5 , 300 ), type= "l" , col= 4 ,lwd= 4 , xlab= "" , ylab= "" )par (new= T)plot (|> filter (x2 <= 5 ) |> _$ x2, |> filter (x2 <= 5 ) |> _$ y2, xlim= c (- 10 , 20 ), ylim= c (- 112.5 , 300 ), type= "l" , col= 4 ,lwd= 0.5 , xlab= "" , ylab= "" )``` `smooth.spline` 関数を用います。`smooth.spline` 関数は`x` (説明変数)、`y` (目的変数)をそれぞれ引数に取り、`smooth.spline` クラスのオブジェクトを返す関数です。`smooth.spline` 関数ではcubic smoothing spline(3次スプライン)という、3次関数を滑らかにつなぎ合わせたspline回帰を行います。このcubic smoothing splineでは、knotとknotの間ごとに3次関数への回帰が最小二乗法で計算されます。ただし、この回帰においては、曲線の曲がり具合(wiggliness)が大きいとペナルティがつくような最小二乗法の計算が行われます。ペナルティの大きさはGCV(Generalized Cross Varidation)という手法で自動的に設定されます。別途`penalty` 変数に数値を設定すると、ペナルティの大きさを調整することができます。大きめの`penalty` を設定すればより滑らかな、小さめの`penalty` を設定すればより曲がりくねった形の回帰となります。`smooth.spline` 関数ではknotの数は自動的に設定される仕組みになっています。```{r, filename="spline回帰"} <- as.data.frame (BJsales) |> mutate (time = 1 : 150 )# スプライン曲線の計算(ペナルティを1.4に設定)、結果にはGCVの結果などが表示される smooth.spline (BJsales_d$ time, BJsales_d$ x, penalty = 1.4 )# 黒線が生データ、赤線がスプライン曲線 plot (BJsales, col = 1 , xlim = c (0 , 150 ), ylim = c (200 , 260 ))par (new = T)smooth.spline (BJsales_d$ time, BJsales_d$ x, penalty = 1.4 ) |> plot (type = "l" , col = 2 , xlim = c (0 , 150 ), ylim = c (200 , 260 ), xlab = "" , ylab = "" )``` ## 加法モデル(additive model) `smooth.spline` 関数を用いた回帰により、滑らかな非線形回帰を行うことができます。このspline回帰を説明変数が複数の場合、つまり重回帰のような場合に拡張したものが**加法モデル**(additive model)です。[ `mgcv` ](https://cran.r-project.org/web/packages/mgcv/) パッケージ[ @mgcv1_bib; @mgcv2_bib; @mgcv3_bib; @mgcv4_bib; @mgcv5_bib ] を用います。`mgcv` では、主に3種類のspline回帰を用いて複雑な非線形回帰を行います。- cubic regression spline:上記の`smooth.spline` で用いられているものと同じものです。knotの間隔はデフォルトでは説明変数の幅を10分割する形で設定されます。knotの位置を最適化すれば、非常に滑らかな非線形回帰を行うことができます。- thin plate regression spline:cubic regression splineと同じく3次関数で非線形回帰を行うspline回帰ですが、knotの位置が自動的に最適化される点が異なります。計算が重く、データ数が多いと時間がかかります。- tensor product spline:複数の説明変数に対して、多次元的なspline回帰を行うための手法です。thin plate regression splineよりも計算が軽いため、データが多い場合に適しています。`mgcv` のデフォルトのspline回帰の手法はthin plate regression splineです。thin plate regression splineはthin plate splineと呼ばれる手法の計算量を小さくしたものです。thin plate spline自体は計算量が大きすぎて使いにくいため、`mgcv` では対応していません。この他にB-splineやP-splineなどの、別のsplineの手法を用いることもできますが、特に理由がない限り使用する必要はないでしょう。thin plate splineに関しては[ こちらの小林景先生(慶應義塾理工学部)のページ ](https://www.math.keio.ac.jp/~kei/GDS/2nd/spline.html) に詳しく記載されています。`smooth.spline` 関数と同じです。ペナルティ付き最小二乗法はP-IRLS(Iteratively Reweighted Least Squares)と呼ばれる繰り返し計算手法で計算します。`smooth.spline` と同じくGCVか、UBRE(Un-biased Risk Estimator)と呼ばれる手法のどちらかで計算されます。特に手法を指定しない場合にはGCVによりGCV-scoreが計算され、GCV-scoreを最小化するペナルティの大きさが決定されます。### 一般化加法モデル(Generalized Additive Model、GAM) ### mgcvでGAMを計算する `mgcv` パッケージでは、`gam` 関数を用いてGAMを計算することができます。`gam` 関数の使い方は`glm` 関数によく似ていますが、説明変数の設定方法が異なります。`mgcv` パッケージでspline回帰を行う場合には、説明変数を`s` 関数の引数に取ります。`trees` )において高さ(`Height` )と直径(`Girth` )から幹の体積(`Volume` )を求める演算をGAMで行っています。説明変数である`Height` と`Girth` は`s` 関数の引数に指定しています。`glm` 関数と同じく、データはデータフレームとして、`data` 引数に指定します。このように指定することで、目的変数-説明変数の関係をsplineによる非線形として設定することができます。`s` 関数内で特に引数を指定しない場合には、thin plate regression splineによる計算が行われます。`gam` 関数の返り値を`plot` 関数の引数に指定することで、各説明変数と目的変数の関係をグラフで示すことができます。グラフの実線は推定値で、点線は信頼区間を示します。x軸に示されている短い縦線はデータの位置を示しています。```{r, filename="gam関数で一般化加法モデルを計算"} :: p_load (mgcv)# s関数に囲まれている説明変数はSpline回帰で演算される <- gam (Volume ~ s (Girth) + s (Height), data = trees)summary (gam_trees)par (mfrow = c (1 , 2 ))plot (gam_trees)``` `s` 関数ではデフォルトの自由度の最大値として10が設定されています。自由度の最大値は`s` 関数内で`k` 引数を指定することで変更することができます。`s` 関数の引数とせずにつなぐことで、その説明変数のみsplineではなく、線形の関係としてモデルに組み込むことができます。`Height` の自由度は1、要は傾きしかない線形であるため、`s` 関数で囲う意味はあまりありません。このような場合には`s` 関数を外して演算すると、説明変数と目的変数の関係がSplineではなく線形として計算されます。```{r, filename="heightのみ線形として演算する"} <- gam (Volume ~ s (Girth) + Height, data = trees)# 線形の成分はplot関数では表示されない plot (gam_trees1)``` ### bs引数でsplineの種類を指定する `airquality` )のうち、オゾン量(`Ozone` )を目的変数、日照(`Solar.R` )、風量(`Wind` )、気温(`Temp` )、5月1日からの日数(`days` )を説明変数とするGAMの計算を行っています。```{r, filename="airqualityのデータをGAMで計算"} :: p_load (mgcv)<- airquality |> mutate (days = 1 : nrow (airquality)) # 前準備 # GAMの演算 <- gam (Ozone ~ s (Solar.R) + s (Wind) + s (Temp) + s (days), data = aq)# s(days)はp値が有意ではない summary (result_gam)par (mfrow = c (2 ,2 ))plot (result_gam, select = 1 );plot (result_gam, select = 2 )plot (result_gam, select = 3 );plot (result_gam, select = 4 )``` `days` の回帰結果がほぼ一定に見えます。つまり、`days` は`Ozone` にほとんど影響を与えていないように見えます。このような説明変数は、GLMのモデル選択やスパース回帰では取り除かれる可能性があります。`step` 関数によるモデル選択を適用することはできません。`gam` では、`step` 関数の代わりに、`s` 関数内で引数を指定することにより、モデル選択ができるようにしています。`s` 関数の`bs` 引数は通常splineの手法を指定するための引数です。`bs="cr"` でcubic regression spline、`bs="tp"` でthin plate regression splineを指定することができます(tensor product splineには`s` とは別の関数が準備されています。後ほど説明します)。`bs` 引数に指定可能な手法は`?smooth.terms` (もしくは[ こちらのページ ](https://stat.ethz.ch/R-manual/R-patched/RHOME/library/mgcv/html/smooth.terms.html) )にまとめられています。また、cubic regression splineを選択した場合には、knotの位置を`knot` 引数で設定することもできます(thin plate regression splineを用いる場合には原理的に`knot` を設定する必要がありません)。`bs` 引数に指定できる手法のうちには、「shrinkageが可能な手法」、というものが含まれています。このshrinkageというのは、`s` 関数の結果をほぼ0とする、つまりスパース回帰のように説明変数を取り除くことができるようにすることを意味します。shrinkageが可能な手法は`"cs"` (cubic regression splineでshrinkage可能な手法)と`"ts"` (thin plate regression splineでshrinkage可能な手法)の2つです。`s` 関数内で`bs="cs"` もしくは`bs="ts"` を指定することで、その説明変数が目的変数に影響を与えていない場合には説明変数からある程度取り除くことができます。`step` 関数やスパース回帰のようには説明変数をうまく取り除けないので、AICなどを用いたモデル選択も行うことになります。`lm` や`glm` と同じく、`AIC` 関数の引数に`gam` の返り値を取ることでAICを計算することができます。`bs` 引数にはcyclicな、始めと終わりの値が同じとなるsplineを指定することもできます。代表的なcyclicな方法は`"cc"` (cubic regression splineのcyclic版)です。時系列などで、ある一定の時期ごとに同じ値に戻るような場合には、`bs="cc"` と指定することでより単純で分かりやすいモデルを選択することができます。```{r, filename="shrinkage可能な手法を用いる"} <- gam (~ s (Solar.R, bs = "ts" ) + s (Wind, bs = "ts" ) + s (Temp, bs = "ts" ) + s (days, bs = "ts" ), data = aq)plot (result_gam, select = 4 ) # daysは残っているが、0付近に集まる # tsのモデルの方がわずかにAICが小さい AIC (result_gam)AIC (result_gam2)``` ### s関数に2つの説明変数を含める `s` 関数それぞれに説明変数を設定していましたが、`s` 関数には2つ以上の説明変数を同時に設定することもできます。下の例では、3つの説明変数を`s` 関数の引数に指定しています。このように指定することで、多次元のスプラインを用いてGAMの計算を行うことができます。`s` 関数の代わりに、`te` 関数を用います。`summary` 関数の結果を見るとわかる通り、複数の説明変数を用いたスプラインを作成すると、結果の解釈はより難しくなる傾向があります。```{r, filename="複数の説明変数を用いたスプライン"} # thin plate regression splineで複数の説明変数を加える <- gam (Volume ~ s (Girth, Height, k = 4 ), data = trees)# tensor product splineで複数の説明変数のsplineを作成 <- gam (Volume ~ te (Girth, Height), data = trees)summary (gam_trees2)summary (gam_trees3)# thin plate regression splineでAICが最も小さい AIC (gam_trees) # thin plate regression spline AIC (gam_trees2) # thin plate regression spline(複数の説明変数をs関数に含める) AIC (gam_trees3) # tensor product spline ``` ### ペナルティの調整 `gamma` 引数を指定します。`gamma` 引数のデフォルトは1で、大きくするとより滑らかな、小さくするとより曲がりくねった結果が得られます。[ 教科書 ](https://www.amazon.co.jp/-/en/Simon-N-Wood/dp/1498728332)[ @mgcv4_bib ] では、この`gamma` を`1.4` に指定するのがよいとされていますので、デフォルトの`gam` 関数ではやや曲がりくねった結果を得られやすいことになります。```{r, filename="ペナルティをgammaで調整する"} # gammaを1.4に指定する <- gam (~ s (Solar.R) + s (Wind) + s (Temp), data = aq,gamma = 1.4 )# gammaを0.1に指定する <- gam (~ s (Solar.R) + s (Wind) + s (Temp), data = aq,gamma = 0.1 )# 左(gamma = 1.4)は滑らか、右(gamma = 0.1)は曲がりくねった結果になる par (mfrow = c (1 , 2 ))plot (result_gam3, select = 1 )plot (result_gam4, select = 1 )``` ### by引数 `s` 関数内では`by` 引数に説明変数を設定することができます。例えばAが目的変数、BとCが説明変数の場合に、`gam(A~s(B, by=C))` と設定すると、数式モデルとしては以下のように、Bによるスプライン回帰にCを掛けた形での回帰を行うことになります。`by` 引数の使い方はわかりにくいのですが、例えば地域ごとの経済状況を非線形回帰する場合に、国によって施策が異なり、国境線を境に大きく経済状況が異なる場合、その施策の有り・無しを1と0の説明変数として`by` 引数に設定すれば、施策の効果を評価した上での回帰を行うことができます。```{r, filename="by引数を設定して評価する", eval=FALSE} <- gam (~ s (Solar.R, by = days), data = aq)``` ### predict関数で予測する `lm` や`glm` と同様に、`gam` でも`predict` 関数により結果の予測値を出力することができます。`predict` 関数の使い方も`lm` や`glm` と類似していて、回帰のオブジェクト(`gam` オブジェクト)と予測したいデータを含むデータフレームを引数に取ります。また、標準誤差は引数に`se.fit=TRUE` と設定することで計算することができます。```{r, message=FALSE, warning=FALSE, filename="predict関数での予測"} <- gam (~ s (Solar.R) + s (Wind), data = aq)<- expand.grid (Solar.R = seq (7 , 334 , by = 1 ),Wind = seq (1.7 , 20.7 , by = 0.1 )predict (result_gam2d, d) |> head (5 ) # ベクターが返ってくる <- cbind (d, pred = predict (result_gam2d, d))# 回帰結果は曲面として得られる(下の図は点の集合になっている) |> :: plot_ly (x = ~ Solar.R, y= ~ Wind, z= ~ pred, size= 0.1 , color= ~ pred``` [ 東京大学の資料 ](https://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2015/dataanalysis/L12.pdf) も参考になりますので、一読されるとよいでしょう。### 一般化加法混合モデル(GAMM) `lme4` や`lmerTest` などのライブラリが必要でしたが、GAMMは`mgcv` パッケージの`gam` 関数を用いて計算することができます。`gam` 関数内では、ランダム効果となる説明変数を`s` 関数内で宣言し、`bs="re"` を引数として設定します。`lmerTest` のように`|` を使ってランダム効果を設定する必要はありません。[ 論文 ](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6542350/pdf/peerj-07-6876.pdf)[ @pedersen2019hierarchical ] に詳しく記載されていますので、一読されることをおすすめいたします。```{r, filename="一般化加法混合モデル:GAMM"} # Pedersen et al. (2019)に記載の例 https://peerj.com/articles/6876/#supplemental-information |> head (5 )plot (CO2)<- transform (CO2, Plant_uo = factor (Plant, ordered = FALSE ))<- gam (log (uptake) ~ s (log (conc), k = 5 , bs = "tp" ) + s (Plant_uo, k = 12 , bs = "re" ), # reはランダム効果 data = CO2, method = "REML" , family = "gaussian" )``` `gratia` パッケージ[ @gratia_bib ] を用いてみます。`gratia` は`gam` の結果を`ggplot2` ベースのグラフにしてくれるライブラリです。```{r, filename="GAMMの結果をプロットする"} :: p_load (gratia) # グラフをggplot2準拠にするパッケージ draw (CO2_modG) # concの効果をプロット ```