25  グラフ作成：低レベルグラフィック関数とグラフィックパラメータ

前章で説明した高レベルグラフィック関数は、少数の引数を与えれば軸や点の位置、グラフの種類等をほぼ自動的に設定してくれる関数です。

一方で、低レベルグラフィック関数は、グラフ上に点や線、文字などを逐次追加していくための関数です。Rでは基本的には高レベルグラフィック関数を用いて大まかなグラフを作成し、追加で説明などを加えたいときには低レベルグラフィック関数を用います。低レベルグラフィック関数の一覧を以下の表1に示します。

表1：低レベルグラフィック関数

関数名	関数の意味
points(x, y)	x, yで指定した場所に点を追加
text(x, y, label)	x, yで指定した場所にlabelで指定したテキストを追加
abline(a, b)	傾きb，切片aの線を追加
abline(h)	hで指定したy軸の位置に横線を追加
abline(v)	vで指定したx軸の位置に縦線を追加
polygon(x, y)	x, yで指定した点をつなぐ形を追加
rect(xleft, ybottom, xright, ytop)	指定したサイズの長方形を追加
symbols(x, y, circles)	x, yで指定した位置に図形（円など）を追加
arrows(x0, y0, x1, y1)	x0, y0の位置からx1, y1の位置までの矢印を追加
legend(x, y, legend)	凡例を追加
title(main, sub)	グラフのタイトルを追加
axis(side)	sideで指定した位置に軸を追加
grid()	グリッド線を追加

25.1 points関数

points関数は、すでに存在するグラフに点を追加するための関数です。points関数はxとyの2つの引数を取り、そのx、yが示す場所に点を追加します。

point関数で点を描画

plot(x = 0, y = 0, type = "n", xlab = "", ylab = "") # 軸だけのプロット
points(x = 0, y = 0) # x=0, y=0に点を追加

25.2 text関数

text関数は、グラフに文字を追加するための関数です。text関数はx、yとlabelの3つの引数を取り、そのx、yが示す場所にlabelsで指定した文字列を追加します。

text関数でテキスト表示

plot(x = 0, y = 0, type = "n", xlab = "", ylab = "")
text(x = 0, y = 0, labels = "added text") # x=0, y=0にテキストを追加

25.3 abline関数

abline関数はグラフに直線を追加するための関数です。abline関数の引数の指定方法には以下の4種類があります。

• 切片（引数a）と傾き（引数b）を指定する
• 横線のy軸の位置（引数h）を指定する
• 縦線のx軸の位置（引数v）を指定する
• 線形回帰の結果（引数coef）を指定する

abline関数で直線を引く

plot(x = 0, y = 0, type = "n", xlab = "", ylab = "")
abline(a = -0.5, b = 2, col = "red") # y = 2 x - 0.5 の線を追加
abline(h = 1, col = "blue") # y = 1 の水平線を追加
abline(v = -1, lty = 2, col = "darkgreen") # x = -1 の縦線（点線）を追加

25.4 多角形・図形・矢印を追加

グラフ上に多角形や長方形、図形、矢印を追加する場合には、それぞれpolygon関数、rect関数、symbols関数、arrows関数を用います。

polygon関数は、引数xとyに数値のベクターを取り、そのベクターで指定したx、yの点を繋げた多角形を追加する関数です。始点と終点が一致していれば閉じた多角形を、一致していなければ閉じていない多角形を描画します。

rect関数は長方形を追加するための関数です。rect関数では、引数xleft、xrightで長方形の左端、右端、引数ybottom、ytopで長方形の下端、上端を指定します。

symbols関数は引数x、yに指定した位置に図形を追加するための関数です。symbols関数で指定できる図形は、円（circles）、正方形（squares）、長方形（rectangles）、星（stars）、温度計（thirmometers）、箱ひげ図（boxplot）です。図形名を引数に取り、数値で図形の詳細を指定することでそれぞれの図形を描画できます。

arrows関数は矢印を追加するための関数です。arrows関数の始めの2つの引数（x0とy0）には矢印の始点の座標を、3つ目と4つ目の引数（x1とy1）には矢印の終点の座標をそれぞれ指定します。

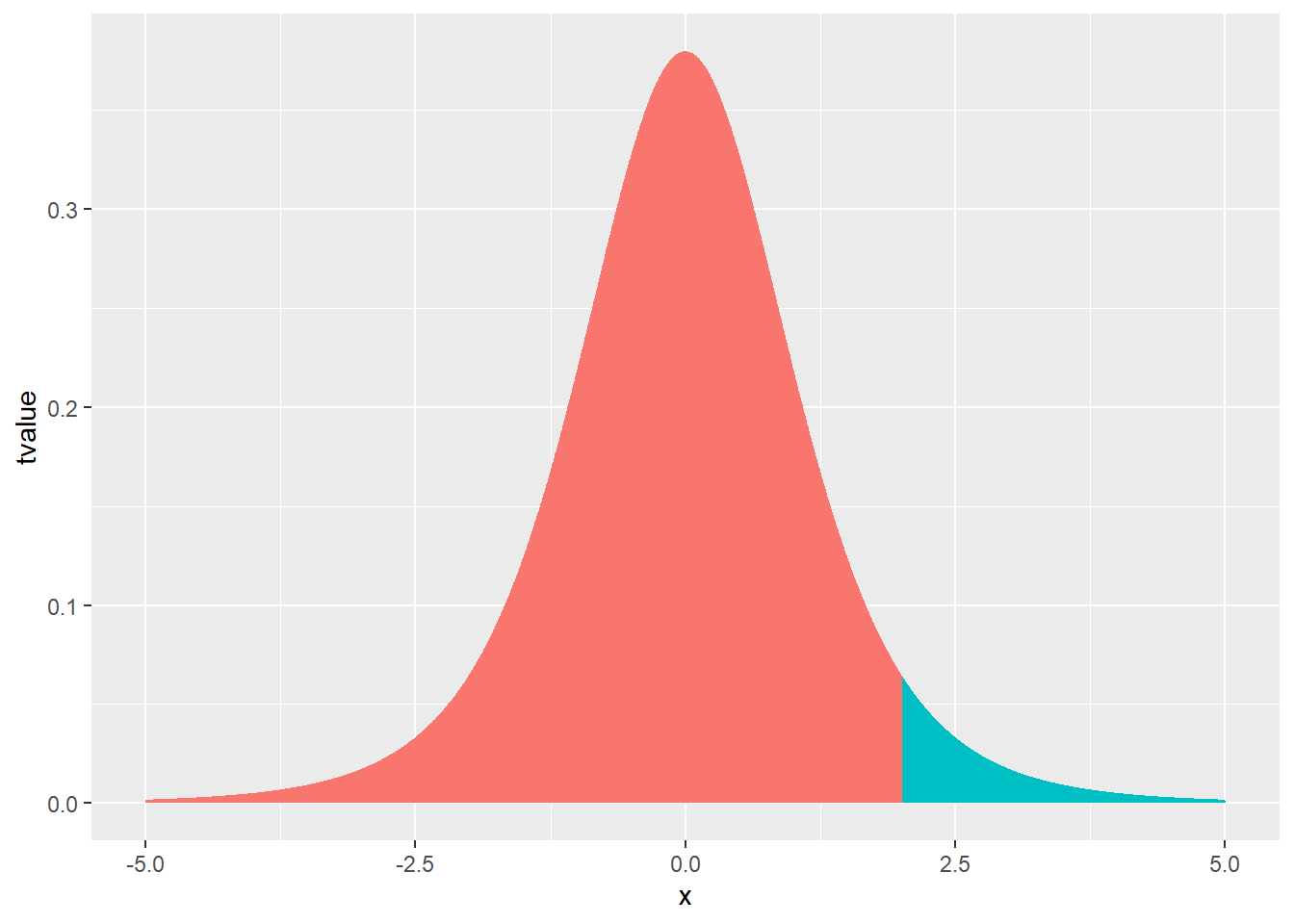
様々な図形の描画

par(mai = c(0.1, 0.1, 0.1, 0.1))
plot(x = 0, y = 0, type = "n", xlab = "", ylab = "", axes = FALSE)
polygon( # 多角形（星形）を追加
  x = c(0, 0.2245, 0.9511, 0.3633, 0.5878, 0, -0.5878, -0.3633, -0.9511, -0.2245, 0, 0.2245) * 0.25 - 0.5,
  y = c(1, 0.309, 0.309, -0.118, -0.809, -0.382, -0.809, -0.118, 0.309, 0.309, 1, 0.309)* 0.25 + 0.5, 
  col = "#48C9B0"
)
# 長方形を追加
rect(xleft = 0, xright = 0.5, ybottom = 0.25, ytop = 0.75, col = "#E74C3C")
# 円を追加
symbols(x = -0.5, y = -0.5, circles = 0.1, add = TRUE, inches = 0.3, col = "#5DADE2")
# 矢印を追加
arrows(x0 = 0.25, y0 = -0.75, x1 = 0.5, y1 = -0.5, col = "#A569BD")

25.5 凡例とタイトルの追加

legend関数は凡例（legend）を追加するための関数です。legend関数はx、y、legendの3つの引数を取り、xとyには凡例の位置を、legendには凡例の説明を示す文字列をそれぞれ引数に取ります。

title関数はグラフのタイトルを追加するための関数です。title関数では、mainとsubの2つの引数にそれぞれメインタイトル、サブタイトルを文字列で指定することで、それぞれのタイトルをグラフに追加することができます。

凡例（legend）とタイトル（title）の表示

plot(x = 0, y = 0, type = "n", xlab = "", ylab = "")
# 凡例（legend）を追加
legend(x = 0.5, y = -0.5, legend = "point", pch = 1)
# タイトルを追加
title(main = "メインタイトル", sub = "サブタイトル")

25.6 軸とグリッドの操作

axis関数はグラフの縦・横軸を追加するための関数です。axis関数の引数は数値の1～4で、1からそれぞれ下・左・上・右の軸の追加を意味します。

グリッド線の追加に用いるのがgrid関数です。grid関数を引数無しで指定すれば、すでに記述されている軸ラベルに従いグリッド線を追加してくれます。引数でグリッドの間隔を指定することもできます。

軸・グリッドの追加

# 軸のないプロットの表示
plot(x = 0, y = 0, type = "n", xlab = "", ylab = "", axes = FALSE)
axis(1) # 下に軸を追加
axis(2) # 左に軸を追加
grid() # グリッドを追加

25.7 グラフィックパラメータ

Rのグラフ作成では、グラフィックパラメータと呼ばれる引数を指定し、点や線、色や軸ラベル等を調整することができます。

グラフィックパラメータはpar関数の引数として用います。plot関数などの高レベルグラフィック関数では、引数として一部のグラフィックパラメータを使用することもできます。Rのグラフィックパラメータは60以上あり、うまく利用すれば見やすく、理解しやすいグラフを作成することもできます。グラフィックパラメータの一覧を以下の表2に示します。

表2：グラフィックパラメータの一覧

グラフィックパラメータ	引数の型	意味	指定の例
adj	数値	文字列の揃えの指定	adj=0（左揃え）、adj=1（右揃え）など
ann	論理型	列ラベルの表示	ann=FALSE
ask	論理型	表示前に入力を求める	ask=TRUE
bg	文字列	背景色	bg=“red”
bty	文字列	軸表示の方法	bty=“l”, bty=“c”など
cex	数値	点の大きさ	cex=2
cex.axis	数値	軸の数値の大きさ	cex.axis=2
cex.lab	数値	軸ラベルの大きさ	cex.lab=2
cex.main	数値	タイトルの大きさ	cex.main=2
cex.sub	数値	サブタイトルの大きさ	cex.sub=2
col	文字列	点の色	col=“blue”
col.axis	文字列	軸の数値の色	col.axis=“green”
col.lab	文字列	軸ラベルの色	col.lab=“orange”
col.main	文字列	タイトルの色	col.main=“yellow”
col.sub	文字列	サブタイトルの色	col.sub=“violet”
crt	数値	文字の回転角度	crt=90
family	文字列	フォントファミリーの指定	familty=“sans”
fg	文字列	枠の色	fg=“yellowgreen”
fig	数値	グラフのデバイス上での位置を指定	fig=c(0, 0.5, 0, 0.5)
fin	数値	グラフのサイズ（幅、高さ、単位はインチ）	fin=c(4, 4)
font	数値	使用するフォント	font=2（太字）, font=3（イタリック）など
font.axis	数値	軸の数値に使用するフォント	font.axis=4（太字イタリック）など
font.lab	数値	軸ラベルに使用するフォント	font.lab=2
font.main	数値	タイトルに使用するフォント	font.main=2
font.sub	数値	サブタイトルに使用するフォント	font.sub=2
lab	数値	軸の数値のおおよその数（x軸、y軸、長さ）	lab=c(4, 4, 8)
las	数値	軸の数値の方向	las=2など
lend	数値	線の端の形	lend=0（丸）, lend=2（角）など
ljoin	数値	線の接続の形	ljoin=0（丸）, ljoin=2（角）など
lmitre	数値	線の接続の形（接続のしかた）	lmitre=5など
lty	数値	線の種類（実線、点線など）	lty=2など
lwd	数値	線の太さ	lwd=2
mai	数値	グラフのマージンの大きさ（インチ）	mai=c(1, 1, 1, 1)など
mar	数値	グラフのマージンの大きさ（ライン）	mar=c(3, 3, 3, 1)など
mex	数値	マージンに依存したフォントサイズの大きさ	mex=2
mfcol, mfrow	数値	デバイスにグラフを複数表示するときの指定	mfcol=c(2,2), mfrow=c(3,2)
mfg	数値	グラフを複数表示するときの表示位置の指定	mfg=c(1, 2)
mgp	数値	表題や軸ラベルと軸との間隔	mgp=c(1, 1, 2) （表題、x軸ラベル、y軸ラベル）
new	論理型	デバイスをクリアせずに描画する	new=T
oma	数値	グラフのマージンの大きさ（文字の行）	oma=c(1, 1, 1, 1)
omd	数値	グラフを複数表示するときのマージンの内側のサイズ（数値は割合）	omd=c(0.1, 0.9, 0.1, 0.9)
omi	数値	グラフを複数表示するときのマージンの大きさ（インチ）	omi=c(1, 1, 1, 1)
pch	数値	グラフの点の大きさ	pch=2
pin	数値	グラフのサイズ（幅、高さ，単位はインチ）	pin=c(4, 4)
plt	数値	現在の図の位置の中でのグラフのサイズ（数値は割合）	plt=c(0.3, 0.5, 0.3, 0.5)
ps	数値	テキストのサイズ（単位はポイント）	ps=16
pty	文字列	グラフの枠の形	pty=“s”（正方形）, pty=“m”（最大）
srt	数値	文字列の角度の指定	srt=90
tck	数値	軸ラベルを示す線の長さ（数値は割合）	tck=0.2
tcl	数値	軸ラベルを示す線の長さ	tcl=1
usr	数値	軸の境界値	usr=c(0, 10, 0, 15)
xaxp	数値	x軸ラベルの位置	xaxp=c(0, 10, 2)（0から10まで2間隔）
xaxs	文字列	x軸ラベルの位置（自動的ラベル付与の設定変更）	xaxs=“r”，xaxs=“I”
xaxt	文字列	x軸の表示方法	xaxt=“n”, xaxt=“s”
xlog	論理型	x軸を対数変換する	xlog=T
xpd	論理型	グラフ・図の切り出し	xpd=TRUE, xpd=NAなど
yaxp	数値	y軸ラベルの位置	yaxp=c(0, 10, 2)（0から10まで2間隔）
yaxs	文字列	y軸ラベルの位置（自動的ラベル付与の設定変更）	yaxs=“r”，yaxs=“I”
yaxt	文字列	y軸の表示方法	yaxt=“n”, yaxt=“s”
ylbias	数値	軸ラベルの文字の位置	ylbias=0.5
ylog	論理型	y軸を対数変換する	ylog=T

25.8 重ね書き：new=T

前章で説明した通り、Rではすでに記述しているグラフに、別のグラフを重ね書きすることができます。この重ね書きに用いるのが、new=Tというグラフィックパラメータです。par(new=T)を宣言すると、宣言前に作図したグラフを消去することなく、同じデバイス上に次のグラフが追加されます。

par(new=T)でグラフの重ね書き

plot(1:10)
par(new = T) # デバイス上のグラフを消去しない
plot(10:1, col = "red") # 赤のプロットを追加

25.9 複数のグラフを1つのデバイスに表示

複数のグラフを1つのデバイス上に描画する場合には、グラフィックパラメータのmfrow引数又はmfcol引数を用います。いずれも引数に2つの数値からなるベクターを取ります。ベクターの1つ目の要素が行方向にデバイスを分割する数、2つ目の要素が列方向にデバイスを分割する数になります。このとき、mfrowとmfcolのいずれを用いても、結果は同じになります。

グラフィックパラメータとしてpar関数内で引数mfrow又はmfcolを宣言した後、plot関数などの高レベルグラフィック関数を用いてグラフを描画します。plot関数では、引数mfgを用いて、グラフを表示する位置を指定します。位置は引数mfrowで指定した行、列の中で設定します。例えば、mfg=c(2, 3)と指定すると、そのグラフはグラフィックデバイスのうち、2行3列目に描画されます。

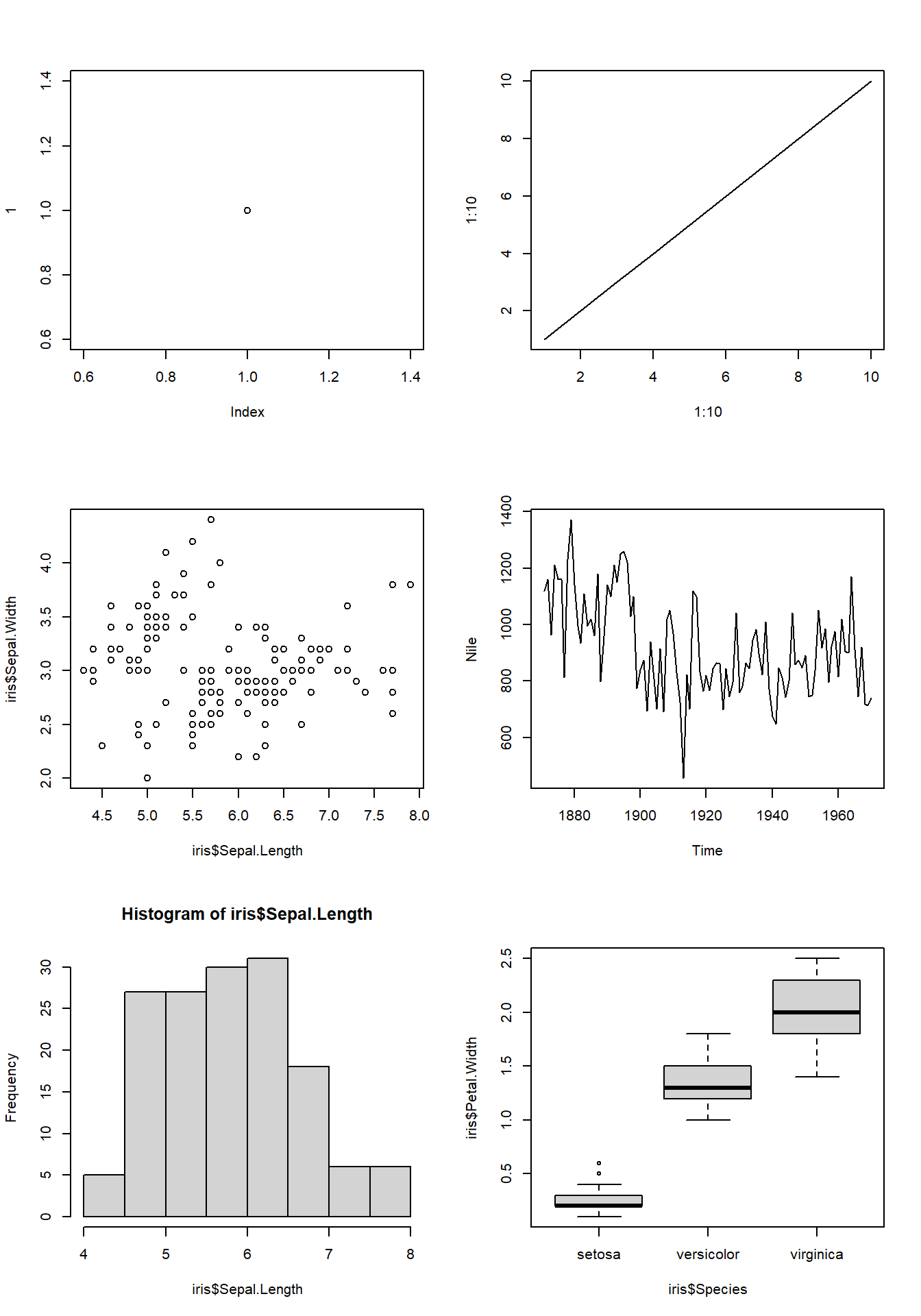
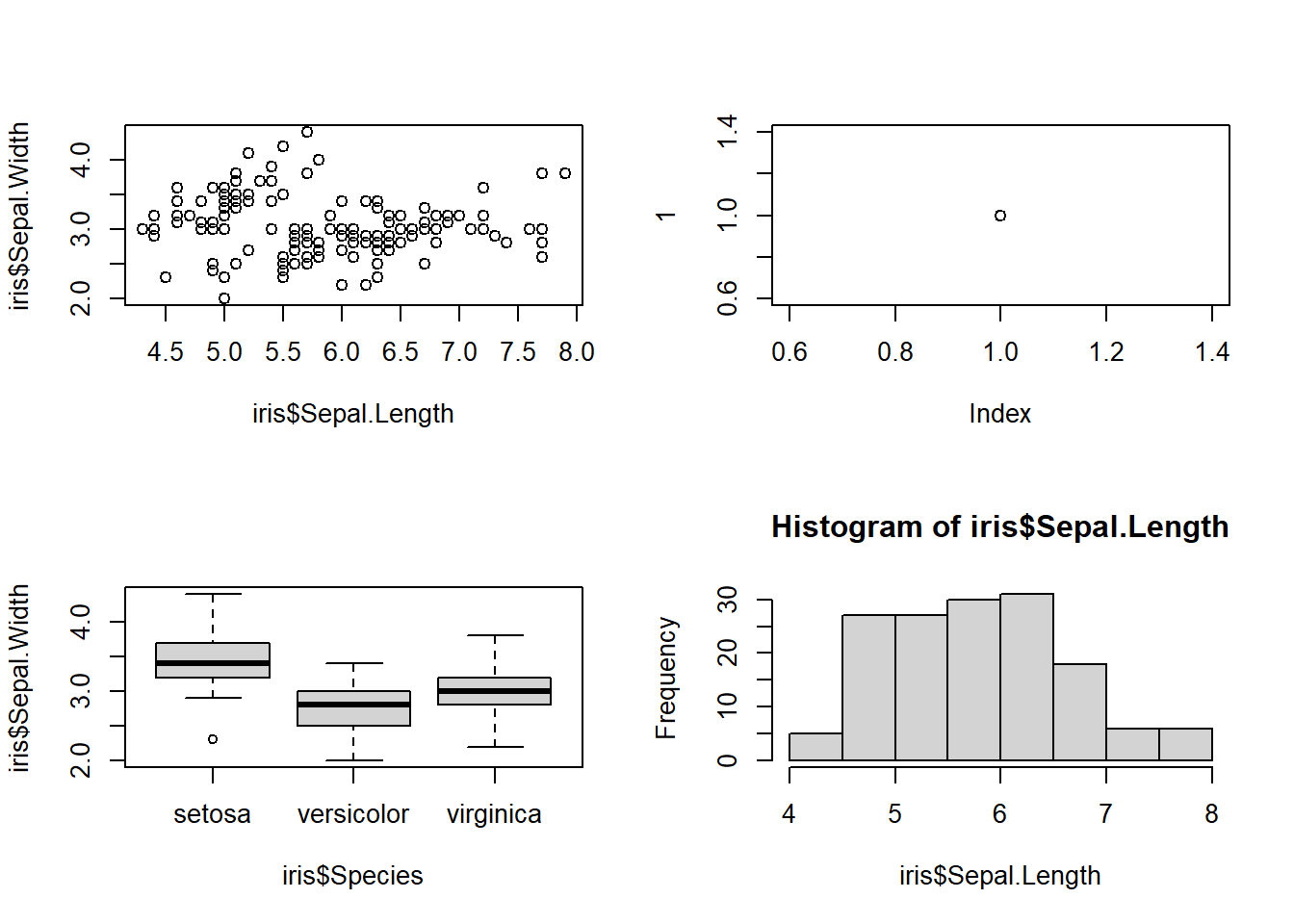
複数のプロットを表示1

# mfcolでもmfrowでも同じ。3行2列にデバイスを分割
par(mfrow = c(3, 2)) 
plot(1, mfg = c(1, 1)) # 1行1列目のグラフ
plot(1:10, 1:10, type = "l", mfg = c(1, 2)) # 1行2列目のグラフ
plot(iris$Sepal.Length, iris$Sepal.Width, mfg = c(2, 1)) # 2行1列目のグラフ
plot(Nile, mfg = c(2, 2))
hist(iris$Sepal.Length, mfg = c(3, 1))
boxplot(iris$Petal.Width~iris$Species, mfg = c(3, 2))

同様のデバイスの分割には、layout関数を用いることもできます。layout関数は行列を引数に取ります。行列の要素は数値で、数値の順にグラフが埋められていきます。

複数のプロットを表示2

layout(matrix(c(2, 4, 1, 3), nrow=2)) # 2行2列に分割
plot(1) # 行列の数値の順番にグラフが描画される
plot(iris$Sepal.Length, iris$Sepal.Width)
hist(iris$Sepal.Length)
boxplot(iris$Sepal.Width~iris$Species)

グラフの分割には、split.screen関数を用いることもできます。split.screen関数は引数に数値2つのベクターを取ります。1要素目の数値が行数、2要素目の数値が列数を示します。split.screen関数では、screen関数によって描画するグラフの位置を指定します。例えば、screen(n=2)を指定すると、分割したデバイスの2番目の位置に次のグラフが描画されることになります。

split.screen関数でプロットエリアを分割

split.screen(c(1, 3)) # 1行3列にデバイスを分割

[1] 1 2 3

plot(1) # 1つ目（一番左）に描画
screen(n = 2) # 2つ目に描画することを指定
plot(iris$Sepal.Length, iris$Sepal.Width)
screen(n = 3)
hist(iris$Sepal.Length)

複数のグラフの表示

Rのデフォルトの関数群を用いても、上記のように複数のグラフを1つのデバイスにまとめることはできます。ただし、上の図に見られるように、各グラフのラベルやサイズ、タイトルなどをうまく調節するためには、グラフィックパラメータを駆使する必要があります。複数のグラフを一度に表示したい場合には、latticeパッケージやggplot2パッケージを用いることで、デフォルトの関数よりも簡単に複数のグラフをまとめて作成することができます。

25.10 マージンの設定

マージン（余白）には、個々のグラフに対するマージンと、デバイスに対するマージンの2つがあります。デバイスにグラフを1つだけ表示する場合には、この2つのマージンは同じ意味を持ちます。

一方で、上で説明した通り、Rではデバイスを分割して複数のグラフを表示することができます。デバイスを分割する場合には、デバイス全体のマージンとは別に、表示する個々のグラフに対するマージンを設定することができます。

個々のグラフに対するマージンを設定するグラフィックパラメータはmai、marです。marとmaiの違いは、maiがマージンをインチ単位で設定するのに対し、marは文字の行で設定する点です。いずれも要素が4つの数値ベクターでマージンを設定します。数値ベクターの要素はそれぞれ下、左、上、右のマージンを表したものとなります。

デフォルトの余白

plot(1)

maiで余白の調整

par(mai = c(2, 2, 2, 2))
plot(1)

デバイス全体のマージンを設定するグラフィックパラメータがomi、omaです。omiとomaの違いはmai、marと同じで、omiがインチ単位、omaが行単位でマージンを設定する引数です。要素が4つの数値ベクターで設定すること、要素がそれぞれ下、左、上、右のマージンを表すのも、mai、marと同じです。

デフォルトの余白

# デフォルトの余白
par(mfcol = c(1, 2))
plot(1)
plot(1:10)

omiで余白の調整

# omiで余白を調整
par(omi = c(1, 1, 1, 1), mfcol = c(1, 2))
plot(1)
plot(1:10)

25.11 グラフの色の調整

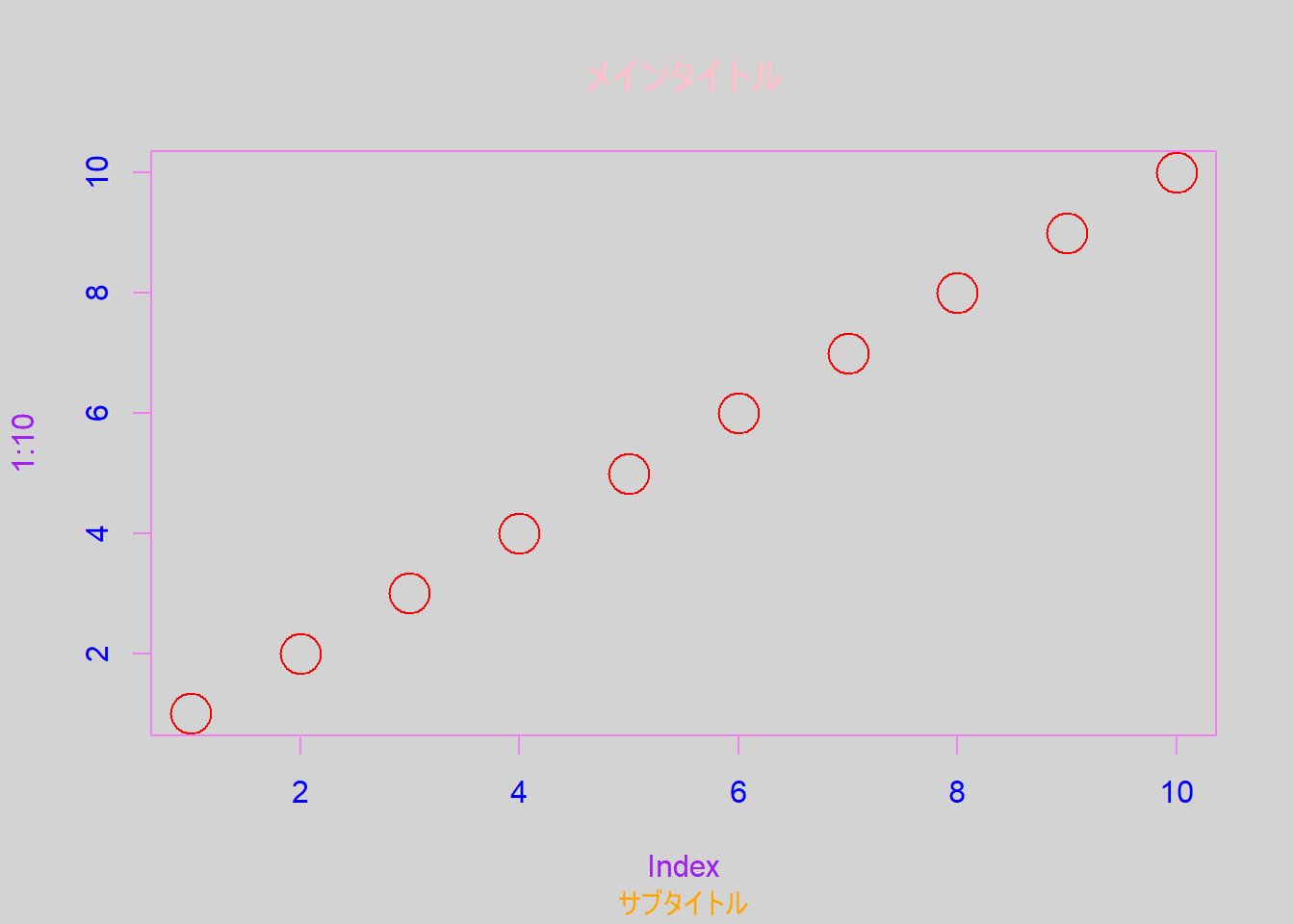
グラフの色も、グラフィックパラメータを用いることで調整することができます。グラフの色に関わるグラフィックパラメータは、bg、col、col.axis、col.lab、col.main、col.sub、fgです。それぞれ、背景色、点の色、軸の色、軸ラベルの色、メインタイトルの色、サブタイトルの色、枠の色を示します。色の設定を用いると、下のようにグラフの要素の色を変えたグラフを作成することもできます。

グラフの色の調整

par(bg = "lightgray") # 背景色はpar関数で呼び出し
plot(
  1:10, 
  cex=3, 
  col = "red", # 点の色は赤
  col.axis = "blue", # 軸の数値は青
  col.lab = "purple", #  軸のラベルは紫
  col.main = "pink", # メインタイトルはピンク
  col.sub = "orange", # サブタイトルはオレンジ
  fg = "violet", # 枠の色はバイオレット
  main = "メインタイトル", 
  sub = "サブタイトル"
  )

Rで用いることのできる色については、NCEAS (National Center for Ecological Analysis and Synthesis)が公開しているチートシートに詳しくまとめられています。

色はベクターで指定することもできます。

ベクターでグラフの色を指定

# Speciesがsetosaなら赤、それ以外は青で表示
plot(
  x = iris$Sepal.Length,
  y = iris$Sepal.Width,
  col = ifelse(iris$Species == "setosa", "red", "blue")
  )

25.12 インタラクティブグラフィック関数

グラフを描画した後、グラフをクリックすることでその点の値を得る場合には、locator関数を用います。locator関数は引数に数値を取り、その数値の回数だけグラフをクリックし、クリックした位置の値を得ることができます。得た値はxとyのリストで返ってきます。

locator関数でクリックした位置の値を取得する

plot(1:10)
locator(1) # 1つの点を選ぶ（xとyの値がリストで返ってくる）

同様に描画したグラフにテキストなどでラベルを表示するための関数が、identify関数です。identify関数は、x、y、labelsの3つの引数を取ります。x、yにはラベルを表示したい位置、labelsにはそれぞれの点に表示するラベルを文字列で記載します。identify関数はRStudioでは正常に機能せず、RGUIでのみ機能します。

identify関数で値を取得する

x <- 1:7
y <- 1:7
plot(x, y)
# 点をクリックすると1~7のラベルが付く（RGUI）
identify(x, y, labels = 1:7)